
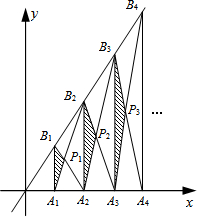
 已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=2x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2 B3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn.若△A1B1P1,△A2B2P2,△A3B3P3,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn为$\frac{{n}^{2}}{2n+1}$.
已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=2x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2 B3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn.若△A1B1P1,△A2B2P2,△A3B3P3,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn为$\frac{{n}^{2}}{2n+1}$. 分析 首先根据OA1=A1A2=A2A3=…=AnAn+1=1,可得OB1=B1B2=B2B3=…=BnBn+1;然后根据三角形的面积公式,求出△OA1B1的面积是1,进而判断出△A1B1B2的面积也是1;再根据A1B1∥A2B2,可得$\frac{{{A}_{1}P}_{1}}{{{P}_{1}B}_{2}}=\frac{{{A}_{1}B}_{1}}{{{A}_{2}B}_{2}}=\frac{1}{2}$,所以${{A}_{1}P}_{1}={{\frac{1}{3}A}_{1}B}_{2}$,所以${S}_{1}={\frac{1}{3}S}_{{{{△A}_{1}B}_{1}B}_{2}}$=$\frac{1}{3}$×$1=\frac{1}{3}=\frac{{1}^{2}}{2×1+1}$;同理,分别判断出S2,S3,…的大小,再总结出一般规律,求出Sn的大小即可.
解答 解:因为OA1=A1A2=A2A3=…=AnAn+1=1,
所以OB1=B1B2=B2B3=…=BnBn+1;
△OA1B1的面积是:
1×(1×2)÷2
=1×2÷2
=1
因为OB1=B1B2,
所以△A1B1B2的面积也是1;
因为A1B1∥A2B2,
所以$\frac{{{A}_{1}P}_{1}}{{{P}_{1}B}_{2}}=\frac{{{A}_{1}B}_{1}}{{{A}_{2}B}_{2}}=\frac{1}{2}$,
所以${{A}_{1}P}_{1}={{\frac{1}{3}A}_{1}B}_{2}$,
所以${S}_{1}={\frac{1}{3}S}_{{{{△A}_{1}B}_{1}B}_{2}}$=$\frac{1}{3}$×$1=\frac{1}{3}=\frac{{1}^{2}}{2×1+1}$;
△OA2B2的面积是:
2×(2×2)÷2
=2×4÷2
=4
因为OB2=2B2B3,
所以△A2B2B3的面积是:
4×$\frac{1}{2}=2$;
因为A2B2∥A3B3,
所以$\frac{{{A}_{2}P}_{2}}{{{P}_{2}B}_{3}}=\frac{{{A}_{2}B}_{2}}{{{A}_{3}B}_{3}}=\frac{2}{3}$,
所以${{A}_{2}P}_{2}={{\frac{2}{5}A}_{2}B}_{3}$,
所以S2=$\frac{2}{5}$×2=$\frac{4}{5}$=$\frac{{2}^{2}}{2×2+1}$;
同理,可得S3=$\frac{9}{7}=\frac{{3}^{2}}{2×3+1}$,
…,
所以Sn=$\frac{{n}^{2}}{2n+1}$.
故答案为:$\frac{{n}^{2}}{2n+1}$.
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力;解答此题的关键是从S1,S2,S3,…的大小总结出Sn的大小.
(2)此题还考查了三角形的面积的求法、三角形的面积大小比较,以及平行线的性质,要熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源: 题型:解答题
 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直接MN交BC于点M,交AD于点N.求证:四边形AMCN是菱形.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直接MN交BC于点M,交AD于点N.求证:四边形AMCN是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,阴影部分(正方形)的四个顶点在5×5的网格格点上.
如图,阴影部分(正方形)的四个顶点在5×5的网格格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
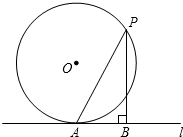 如图,直线l与半径为3的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连结PA,设PA=m,PB=n,则m-n的最大值是( )
如图,直线l与半径为3的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连结PA,设PA=m,PB=n,则m-n的最大值是( )| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又散步走回家,图中x表示时间,y表示张强离家的距离.则下列说法错误的是( )
如图图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又散步走回家,图中x表示时间,y表示张强离家的距离.则下列说法错误的是( )| A. | 体育场离张强家2.5km | |
| B. | 张强从家到体育场用了15min | |
| C. | 张强在体育场锻炼了15min | |
| D. | 张强散步回家的平均速度是2.5km/h |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,点是AB上的一个动点(不与A,B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,点是AB上的一个动点(不与A,B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况( )| A. | 先增大后减少 | B. | 先减少后增大 | C. | 逐渐增大 | D. | 逐渐减少 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
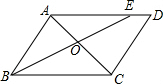 如图,在平行四边形ABCD中,点E在AD上,已知AE=3ED=6cm,OC=4cm,则AC的长为( )
如图,在平行四边形ABCD中,点E在AD上,已知AE=3ED=6cm,OC=4cm,则AC的长为( )| A. | 9cm | B. | 7cm | C. | 6cm | D. | 8cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com