
如图1,已知直线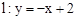 与y轴交于点A,抛物线
与y轴交于点A,抛物线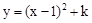 经过点A,其顶点为B,另一抛物线
经过点A,其顶点为B,另一抛物线 的顶点为D,两抛物线相交于点C
的顶点为D,两抛物线相交于点C
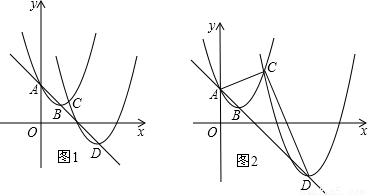
(1)求点B的坐标,并说明点D在直线 的理由;
的理由;
(2)设交点C的横坐标为m
①交点C的纵坐标可以表示为: 或 ,由此请进一步探究m关于h的函数关系式;
②如图2,若 ,求m的值
,求m的值
(1)B(1,1)(2)①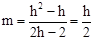 ②
②
【解析】解:(1)当x=0时候, ,∴A(0,2)。
,∴A(0,2)。
把A(0,2)代入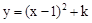 ,得1+k=2,∴k=1。∴B(1,1)。
,得1+k=2,∴k=1。∴B(1,1)。
∵D(h,2-h),∴当x=h时, 。
。
∴点D在直线l上。
(2)① 或
或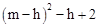 。
。
由题意得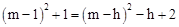 ,整理得
,整理得 。
。
∵h>1,∴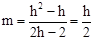 。
。
②过点C作y轴的垂线,垂足为E,过点D作DF⊥CE于点F,

∵∠ACD=90°,∴∠ACE=∠CDF。
又∵∠AEC=∠DFC,∴△ACE∽△CDF。∴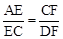 。
。
又∵C(m, ),D(2m,2-2m),
),D(2m,2-2m),
∴AE= ,DF=
,DF= ,CE=CF=m。
,CE=CF=m。
∴ 。∴
。∴ =1。
=1。
解得: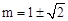 。
。
∵h>1,∴ 。∴
。∴ 。
。
(1)首先求得点A的坐标,然后求得点B的坐标,用h表示出点D的坐标后代入直线的解析式验证即可。
(2)根据两种不同的表示形式得到m和h之间的函数关系即可;过点C作y轴的垂线,垂足为E,过点D作DF⊥CE于点F,证得△ACE∽△CDF,然后用m表示出点C和点D的坐标,根据相似三角形的性质求得m的值即可。


科目:初中数学 来源: 题型:
如图(a)过反比例函数![]() 的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S
的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S![]() 与S
与S![]() ,
,
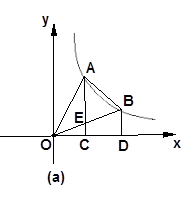

1.试比较S![]() 与S
与S![]() 的大小;
的大小;
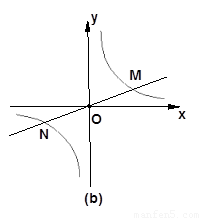
2.如图(b),已知直线![]() 与双曲线
与双曲线![]() 交于M、N点,且点M的纵坐标为2.
交于M、N点,且点M的纵坐标为2.
①求m的值;
②若过原点的另一条直线l交双曲线于P、Q两点(P点在第一象限),若由M、N、P、Q为顶点组成的四边形面积为64,求P点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
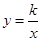 的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S
的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S 与S
与S ,
,

 与S
与S 的大小;
的大小;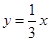 与双曲线
与双曲线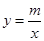 交于M、N点,且点M的纵坐标为2.
交于M、N点,且点M的纵坐标为2.查看答案和解析>>
科目:初中数学 来源:2011年福建省泉州市南安市初中毕业班数学综合练习卷(二)(解析版) 题型:解答题
 与双曲线
与双曲线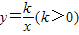 交于A、B两点,且点A的横坐标为4.
交于A、B两点,且点A的横坐标为4. 于C、D两点(点C在第一象限且在点A的左边),当四边形ACBD的面积为24时,求点C的坐标.
于C、D两点(点C在第一象限且在点A的左边),当四边形ACBD的面积为24时,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源:2011年重庆名校中考数学函数综合试题精练 题型:选择题
如图(a)过反比例函数 的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S
的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S 与S
与S ,
,

1.试比较S 与S
与S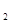 的大小;
的大小;
2.如图(b),已知直线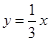 与双曲线
与双曲线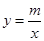 交于M、N点,且点M的纵坐标为2.
交于M、N点,且点M的纵坐标为2.
①求m的值;
②若过原点的另一条直线l交双曲线于P、Q两点(P点在第一象限),若由M、N、P、Q为顶点组成的四边形面积为64,求P点的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com