
| 100 |
| π |
 解:(1)设矩形长为x,宽为y,
解:(1)设矩形长为x,宽为y,| 400-2x |
| π |
| 400-2x |
| π |
| 1 |
| π |
| 400 |
| 2×(-2) |
| 100 |
| π |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
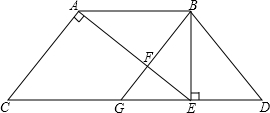 如图,在等腰梯形ABDC中,AC=BD,AB∥CD,过点B作BE⊥CD,垂足为E,连接AE,且∠CAE=90°,若∠ABF=∠D,
如图,在等腰梯形ABDC中,AC=BD,AB∥CD,过点B作BE⊥CD,垂足为E,连接AE,且∠CAE=90°,若∠ABF=∠D,查看答案和解析>>
科目:初中数学 来源: 题型:
 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-| 1 |
| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com