
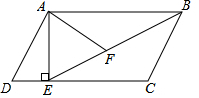
 如图,在?ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
如图,在?ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.分析 (1)由平行四边形的性质得出AB∥CD,AD∥BC,AD=BC,得出∠D+∠C=180°,∠ABF=∠BEC,证出∠C=∠AFB,即可得出结论;
(2)由勾股定理求出BE,由三角函数求出AE,再由相似三角形的性质求出AF的长.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AD=BC,
∴∠D+∠C=180°,∠ABF=∠BEC,
∵∠AFB+∠AFE=180°,
∴∠C=∠AFB,
∴△ABF∽△BEC;
(2)解:∵AE⊥DC,AB∥DC,
∴∠AED=∠BAE=90°,
在Rt△ABE中,根据勾股定理得:BE=$\sqrt{A{E}^{2}+A{B}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
在Rt△ADE中,AE=AD•sinD=5×$\frac{4}{5}$=4,
∵BC=AD=5,
由(1)得:△ABF∽△BEC,
∴$\frac{AF}{BC}=\frac{AB}{BE}$,即$\frac{AF}{5}=\frac{8}{4\sqrt{5}}$,
解得:AF=2$\sqrt{5}$.
点评 此题考查了相似三角形的判定与性质,以及平行四边形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 方式 | 频数 | 百分比 |
| 网络 | 23 | 46% |
| 电视 | ||
| 报纸 | 8% | |
| 其他 | 15 | |
| 合计 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
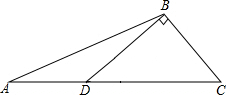 如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)
如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.
如图,矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
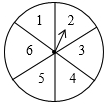 如图,一个质地均匀的转盘被平均分成6等份,分别标有数字1,2,3,4,5,6,当它停止时,指针指向的数字即为转出的数字(若指针指在分界线上,则重新转动转盘).小颖与小亮进行转盘游戏,规则是:若转出的数是3的倍数则小颖获胜,若不是3的倍数则小亮获胜.
如图,一个质地均匀的转盘被平均分成6等份,分别标有数字1,2,3,4,5,6,当它停止时,指针指向的数字即为转出的数字(若指针指在分界线上,则重新转动转盘).小颖与小亮进行转盘游戏,规则是:若转出的数是3的倍数则小颖获胜,若不是3的倍数则小亮获胜.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com