
【题目】已知:抛物线C1:y=x2-2a x+2a+2 顶点P在另一个函数图象C2上,
(1)求证:抛物线C1必过定点A(1,3);并用含的a式子表示顶点P的坐标;
(2)当抛物线C1的顶点P达到最高位置时,求抛物线C1解析式;并判断是否存在实数m、n,当m≤x≤n时恰有3m≤y≤3n,若存在,求出求m、n的值;若不存在,说明理由;
(3)抛物线C1和图象C2分别与y轴交于B、C点,当△ABC为等腰三角形,求a的值.
【答案】(1)顶点P(a,-a 2+2a+2) (2)m=1, n=4 (3)![]() ,或
,或![]() ,或a =1,a =0(B与C重合,舍去)
,或a =1,a =0(B与C重合,舍去)
【解析】试题分析:(1)根据待定系数法,直接把A点的坐标x=1代入即可证明抛物线C1必过定点A,然后根据配方法求出顶点P的坐标;
(2)先根据配方法求出yP=-(a-1) 2+3≤3,得到P的最高点的坐标,求得C1解析式,然后根据二次函数的最值以及二次函数的增减性可求出m、n的值;
(3)分别求出两函数和y轴的交点,然后结合等腰三角形和勾股定理分类讨论即可求出a的值.
试题解析:(1)∵当![]() 时,
时, ![]()
∴ 抛物线C1必过定点A(1,3)
∵抛物线C1:y=x2-2a x+2a+2=(x-a)2-a 2+2a+2
∴顶点P(a,-a 2+2a+2)
(2)∵yP=-a 2+2a+2=-(a-1) 2+3≤3
∴当![]() 时,P达到最高位置(1,3)
时,P达到最高位置(1,3)
此时抛物线C1解析式为y=x2-2 x+4
∴ y=x2-2 x+4=(x-1)2+3 ≥3
∵当m≤x≤n时恰有3m≤y≤3n
∴3≤3m≤y≤3n
∴1≤m≤n
∴当1≤m≤x≤n ,y随x的增大面增大
∴当x= m 时, y= 3m,当x= n 时,y= 3 n
∴![]() 解得
解得![]()
∵ 1≤m≤n
∴m=1, n=4
(3)∵抛物线C1:y=x2-2a x+2a+2与y轴交于B点
∴B(0,2a+2)
∵函数yP=-x 2+2x+2图象C2与y轴交于C点
∴C(0,2)
∵A(1,3)
∴由勾股定理得AC=![]() ,BC =
,BC = ![]() ,AB2=( a -1) 2+1
,AB2=( a -1) 2+1
∵△ABC为等腰三角形
∴①AC=BC ②BC 2= AB2 ③AC 2= AB2
∴![]() =
=![]() 或 4 a 2 =(2 a -1) 2+1 或2= (2 a -1) 2+1
或 4 a 2 =(2 a -1) 2+1 或2= (2 a -1) 2+1
∴![]() ,或
,或![]() ,或a =1,a =0(B与C重合,舍去)
,或a =1,a =0(B与C重合,舍去)


科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 图像的一部分,其对称轴为x=-l,且过点(-3,0).下列说法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1),
图像的一部分,其对称轴为x=-l,且过点(-3,0).下列说法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1),![]() 是抛物线上两点,则y1>y2,其中说法正确的有( )
是抛物线上两点,则y1>y2,其中说法正确的有( )
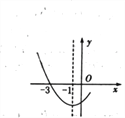
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为______.
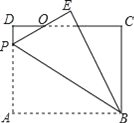
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA′=CA,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).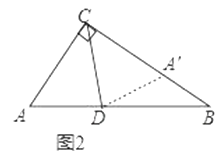
请回答:
(1)在图2中,小明得到的全等三角形是△≌△;
(2)求BC和AC、AD之间的数量关系是
(3)参考小明思考问题的方法,解决问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9.求AB的长.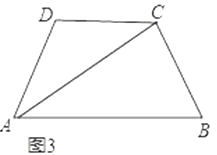
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别 | A型 | B型 | AB型 | O型 |
频率 | 0.4 | 0.35 | 0.1 | 0.15 |
A.16人
B.14人
C.4人
D.6人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是_____海里(不近似计算).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com