
【题目】如图1,在平面直角坐标系中,抛物线![]() 交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
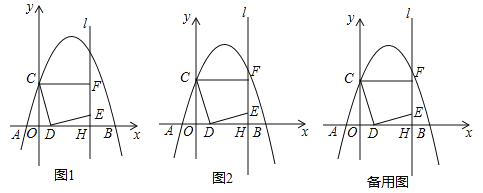
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)1;(3)①
;(2)1;(3)①![]() ;②G(4,
;②G(4,![]() )或(4,6).
)或(4,6).
【解析】
(1)把A、B的坐标代入抛物线的解析式,解方程组即可;
(2)由C的纵坐标求得F的坐标,由△OCD≌△HDE,得出DH=OC=3,即可求得OD的长;
(3)①先确定C、D、E、F四点共圆,由圆周角定理求得∠ECF=∠EDF,由tan∠ECF=![]() =
=![]() ,得到tan∠FDE=
,得到tan∠FDE=![]() ;
;
②连接CE,得出△CDE是等腰直角三角形,∠CED=45°,过D点作DG1∥CE,交直线l于G1,过D点作DG2⊥CE,交直线l于G2,则∠EDG1=45°,∠EDG2=45°,求得直线CE的解析式为![]() ,设直线DG1的解析式为
,设直线DG1的解析式为![]() ,设直线DG2的解析式为
,设直线DG2的解析式为![]() ,把D的坐标代入即可求得m、n,从而求得解析式,进而求得G的坐标.
,把D的坐标代入即可求得m、n,从而求得解析式,进而求得G的坐标.
(1)如图1,∵抛物线![]() 交x轴于A(﹣1,0)和B(5,0)两点,∴
交x轴于A(﹣1,0)和B(5,0)两点,∴![]() ,解得:
,解得: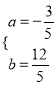 ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)如图2,∵点F恰好在抛物线上,C(0,3),∴F的纵坐标为3,把y=3代入![]() 得,
得,![]() ,解得x=0或x=4,∴F(4,3),∴OH=4,∵∠CDE=90°,∴∠ODC+∠EDH=90°,∴∠OCD=∠EDH,在△OCD和△HDE中,∵∠OCD=∠EDH,∠COD=∠DHE=90°,CD=DE,∴△OCD≌△HDE(AAS),∴DH=OC=3,∴OD=4﹣3=1;
,解得x=0或x=4,∴F(4,3),∴OH=4,∵∠CDE=90°,∴∠ODC+∠EDH=90°,∴∠OCD=∠EDH,在△OCD和△HDE中,∵∠OCD=∠EDH,∠COD=∠DHE=90°,CD=DE,∴△OCD≌△HDE(AAS),∴DH=OC=3,∴OD=4﹣3=1;
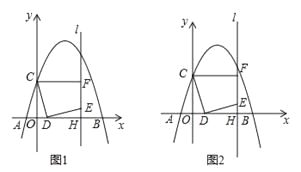
(3)①如图3,连接CE,∵△OCD≌△HDE,∴HE=OD=1,∵BF=OC=3,∴EF=3﹣1=2,∵∠CDE=∠CFE=90°,∴C、D、E、F四点共圆,∴∠ECF=∠EDF,在RT△CEF中,∵CF=OH=4,∴tan∠ECF=![]() =
=![]() ,∴tan∠FDE=
,∴tan∠FDE=![]() ;
;
②如图4,连接CE,∵CD=DE,∠CDE=90°,∴∠CED=45°,过D点作DG1∥CE,交直线l于G1,过D点作DG2⊥CE,交直线l于G2,则∠EDG1=45°,∠EDG2=45°,∵EH=1,OH=4,∴E(4,1),∵C(0,3),∴直线CE的解析式为![]() ,设直线DG1的解析式为
,设直线DG1的解析式为![]() ,∵D(1,0),∴
,∵D(1,0),∴![]() ,解得m=
,解得m=![]() ,∴直线DG1的解析式为
,∴直线DG1的解析式为![]() ,当x=4时,
,当x=4时,![]() =
=![]() ,∴G1(4,
,∴G1(4,![]() );
);
设直线DG2的解析式为![]() ,∵D(1,0),∴0=2×1+n,解得n=﹣2,∴直线DG2的解析式为
,∵D(1,0),∴0=2×1+n,解得n=﹣2,∴直线DG2的解析式为![]() ,当x=4时,y=2×4﹣2=6,∴G2(4,6);
,当x=4时,y=2×4﹣2=6,∴G2(4,6);
综上,在直线l上,是否存在点G,使∠EDG=45°,点G的坐标为(4,![]() )或(4,6).
)或(4,6).


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=4,点P是CB边上的一点,且tan∠PAC=![]() ,⊙O是△APB的外接圆.
,⊙O是△APB的外接圆.
(1)求证:∠PAC=∠ABC;
(2)求证:AC是⊙O的切线;
(3)求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() 为
为![]() 的中点,一块足够大的三角板的直角顶点与点
的中点,一块足够大的三角板的直角顶点与点![]() 重合,将三角板绕点
重合,将三角板绕点![]() 旋转,三角板的两直角边分别交
旋转,三角板的两直角边分别交![]() 或它们的延长线)于点
或它们的延长线)于点![]() ,设
,设![]() ,下列四个结论:①
,下列四个结论:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() ,正确的个数是( )
,正确的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知:点A(﹣4,0),B (0,3)分别是x、y轴上的两点.
(1)用尺规作图作出△ABO的外接圆⊙P;(不写作法,保留作图痕迹)
(2)求出⊙P向上平移几个单位后与x轴相切.
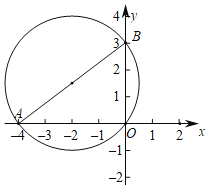
查看答案和解析>>
科目:初中数学 来源: 题型:
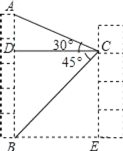
【题目】小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.

(1)求证:BD是⊙O的切线.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为8,cos∠BFA=![]() ,求△ACF的面积.
,求△ACF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
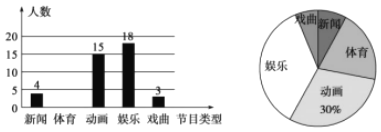
请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
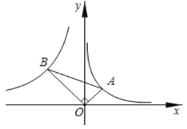
【题目】如图,Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y=![]() (x>0)与y=
(x>0)与y=![]() (x<0)的图象上,则tan∠BAO的值为 ____.
(x<0)的图象上,则tan∠BAO的值为 ____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com