
����Ŀ�����Ķ��������ϣ�
������ʽ�ķ�������������������������n����Ȼ����a0��������a1��a2��a3������an����������

����![]() ��Ϊ�����̡�
��Ϊ�����̡�
�������·�ʽ�ɽ��κ�һ������ת��Ϊ����������ʽ��![]() ����
����![]() ������
������![]() �ĵ�������
�ĵ�������![]() ���Ӷ�
���Ӷ� ���ٿ���
���ٿ���![]() �ĵ�������
�ĵ�������![]() �����ǵõ�a��������չ��ʽ������4�������̣�3��1��3��3��
�����ǵõ�a��������չ��ʽ������4�������̣�3��1��3��3��

�����������������Ԫһ�β������̵�����⣬��![]() Ϊ�������Ƚ�
Ϊ�������Ƚ�![]() д������������ʽ��������ʾ����Σ��������̵ĸ�����������ż���������̣������������������������㵹���ڶ�����������
д������������ʽ��������ʾ����Σ��������̵ĸ�����������ż���������̣������������������������㵹���ڶ����������� ���Ӷ�
���Ӷ�![]() ��һ���ؽ⡣
��һ���ؽ⡣
���Dz�������![]() ���Ƚ�
���Ƚ�![]() д������������ʽ��
д������������ʽ�� ��
��
ע����������������������̣���֮��дΪż���������̵���ʽ��

���㵹���ڶ������������� ������
������![]() ��
��![]() ��һ���ؽ⡣
��һ���ؽ⡣
���ڷ�ʽ�������Ƶ�����ʽ�ĸ�����ý�����չ��Ϊ�������ķ��������Խ���ʽչ��Ϊ����ʽ������![]() ������ʽչ��ʽ���£�����3�������̣�
������ʽչ��ʽ���£�����3�������̣�![]()
![]() ��
��

�����磬 ������4�������̣�1��
������4�������̣�1��![]() ��
��
���Ķ��������ϣ������������ķ��������������������
��1���ҳ���������x�Ķ���ʽp��q��ʹ��![]() ��
��
��2���ҳ���������x�Ķ���ʽu��v��ʹ��![]() ��
��
���𰸡���1��p��x��q��x+1����2��u��x+1��v��x2+2x.
��������
��1������������Խ���Ŀ�е�ʽ�ӷ�ʽչ��Ϊ����ʽ��Ȼ��Ҫ��������㵹���ڶ���������ʽ�����ɵõ��������x�Ķ���ʽp��q��
��2������������Խ���Ŀ�е�ʽ�ӷ�ʽչ��Ϊ����ʽ��Ȼ��Ҫ��������㵹���ڶ���������ʽ������������x�Ķ���ʽu��v����
�⣺��1��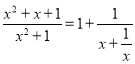 ��
��
���㵹���ڶ�������������![]() ��
��
��p��x��q��x+1��
��2��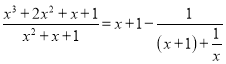 ��
��
���㵹���ڶ�������������![]() ��
��
��u��x+1��v��x2+2x.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=3ax2+2bx+c��
��1����a=3k��b=5k��c=k+1����˵�����ຯ��ͼ���е����ʣ�
��2����a=![]() �� c=2+b���������ک�2��x��2�����ϵ���Сֵ�ǩ�3����b��ֵ��
�� c=2+b���������ک�2��x��2�����ϵ���Сֵ�ǩ�3����b��ֵ��
��3����a+b+c=1���Ƿ����ʵ��x��ʹ����Ӧ��y��ֵΪ1����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��������ABCD��AD�ϣ�����PB������B��һ���������DC���ӳ��߽��ڵ� Q��ʹ�á�QBE=��PBC������E�DZ�AB�ӳ����ϵĵ㣬����PQ����PQ=PB+PD+3������PAB�����Ϊ____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺���ݡ��й���·�г��ڷ�չ�滮����Ԥ�Ƶ�2020��ף��ҹ�����Ǽʹ����ͨ�Ĺ������ǿ���ר�ߵ�2�������н���Ǽʹ����ͨԼͶ��8000��Ԫ������ר��ԼͶ��3500��Ԫ�����˽⣬����ÿ����Ǽʹ����ͨ�����ר�߹���1.5��Ԫ��Ԥ�Ƶ�2020��ף��ҹ�������Ǽʹ����ͨ�Ϳ���ר�߷ֱ�Լ���ٹ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �DZ߳�Ϊ1�������Σ�
�DZ߳�Ϊ1�������Σ�![]() ��
��![]() ��������ļн�Ϊ15�㣬��
��������ļн�Ϊ15�㣬��![]() ��������
��������![]() ��ͼ���ϣ���
��ͼ���ϣ���![]() ��ֵΪ�� ��
��ֵΪ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P������AB���Ϸ�������PAB=45�㣬PA=2����M������AB�ϵĶ���(��M�����A�غ�)���ֽ���P�Ƶ�A��˳ʱ�뷽����ת60������Q������M�Ƶ�P����ʱ�뷽����ת60������N������AQ��PM��PN����ֱ��QN.
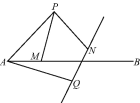
(1)��֤:AM=QN.
(2)ֱ��QN���Ե�PΪԲ������PN�ij�Ϊ�뾶��Բ�Ƿ�������е����?���������������ʱAM�ij���������������˵������.
(3)���Ե�PΪԲ������PN�ij�Ϊ�뾶��Բ������Qʱ��ֱ��д���ӻ�NQ�������뾶��Χ�ɵ����ε����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲μ�����������Сѧ����ʫ�ʴ������ijУ���꼶������ѧ��������Ԥѡ�����а���ǰ5��ѧ���ijɼ����ٷ��ƣ��ֱ�Ϊ���ˣ�l���� 86��85��77��92��85���ˣ�2���� 79��85��92��85��89��ͨ�����ݷ������б����£�
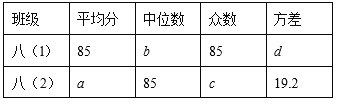
��1��ֱ��д������a��b��c��d��ֵ��
��2�������������ݷ���������Ϊ�ĸ���ǰ5��ͬѧ�ijɼ��Ϻã�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ���һԪ���η���x2��2x��1��0ʱ�����Dz��õ�һ�ַ�������ֱ������ϵ�л���������y��x2��ֱ��y��2x��1����ͼ��ĺ�������Ǹ÷��̵Ľ⣮
(1)���ٸ���һ������ͼ����x2��2x��1��0�Ľ�ķ�����
(2)��֪����y��x3��ͼ��(��ͼ)����x3��x��2��0�Ľ�(���������λ��Ч����)��
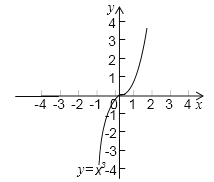
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�D��BC�е㣬����D��ֱ��GF��AC��F����AC��ƽ����BG��G��DE��DF����AB��E,����BG�������ж�BE+CF��EF�Ĵ�С��ϵ����˵������.
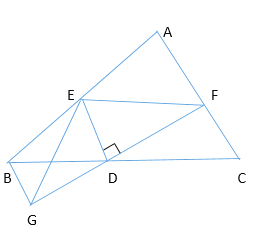
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com