
【题目】在数轴上,A所表示的数为3,点B所表示的数为4,若⊙A的半径为2,则点B与⊙A的位置关系是_____
科目:初中数学 来源: 题型:
【题目】将抛物线y=﹣2x2+1向右平移1个单位,再向下平移3个单位后所得到的抛物线为( )
A.y=-2(x+1)2-2B.y=-2(x+1)2-4C.y=-2(x-1)2-2D.y=-2(x-1)2-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:
在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,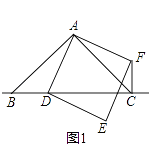
①BC与CF的位置关系为: ,
②BC,DC,CF之间的数量关系为:;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,(1)中的①,②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.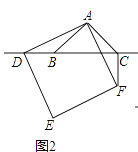
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2,CD=BC,请直接写出GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个学员在广场上驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )
A. 第一次向右拐 50 ,第二次向左拐130
B. 第一次向右拐 50 ,第二次向右拐130
C. 第一次向左拐 50 ,第二次向左拐130
D. 第一次向左拐 30 ,第二次向右拐 30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 上,同时,抛物线
上,同时,抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 上,那么,我们称抛物线
上,那么,我们称抛物线![]() 与
与![]() 关联.
关联.
(1)已知抛物线![]() ,判断下列抛物线:①
,判断下列抛物线:①![]() ;②
;②![]()
![]() 与已知抛物线是否关联,并说明理由;
与已知抛物线是否关联,并说明理由;
(2)已知抛物线![]() :
: ![]() ,点P的坐标为
,点P的坐标为![]() ,将抛物线绕点
,将抛物线绕点![]() 旋转180°得到抛物线
旋转180°得到抛物线![]() (此处我们称点P为旋转点),若抛物线
(此处我们称点P为旋转点),若抛物线![]() 与
与![]() 关联,求抛物线
关联,求抛物线![]() 的解析式;
的解析式;
(3)在(2)的条件下,已知点![]() 是抛物线
是抛物线![]() 上的一点,求以点A为顶点并与抛物线
上的一点,求以点A为顶点并与抛物线![]() 相关联的抛物线
相关联的抛物线![]() 的解析式,并判断此时抛物线
的解析式,并判断此时抛物线![]() 能否由抛物线
能否由抛物线![]() 旋转得来?若能,请求出旋转点坐标;若不能,请说明你的理由;
旋转得来?若能,请求出旋转点坐标;若不能,请说明你的理由;
(4)由上述结论猜想:若两抛物线![]() 相关联,则它们的二次式项系数(分别记为
相关联,则它们的二次式项系数(分别记为![]() )应满足数量关系: .
)应满足数量关系: .
参考公式(中点坐标公式):若点![]() ,则线段AB的中点坐标为
,则线段AB的中点坐标为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
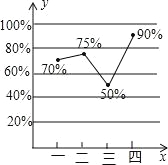
【题目】某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:
(1)若第一季度的汽车销售量为2100辆,求该季的汽车产量;
(2)圆圆同学说:“因为第二,第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说的对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从一个货站向一条高速路修一条最短的公路,其中运用的数学原理是( )
A.在同一平面内,过一点有且只有一条直线垂直于已知直线B.两点之间线段最短
C.连接直线外一点与直线上各点的所有线段中,垂线段最短D.两点确定一条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=900,点A、C的坐标分别为A(-2,0),C(1,0),tan∠BAC=![]() .
.
(1)求点B的坐标。
(2)在x轴上找一点D,连接DB,使得△BCD与△ABC相似(不包括全等),并求点D的坐标。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com