
【题目】已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF.请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可).

(1)连接 ;
(2)猜想: = ;
(3)证明:
【答案】(1)连结AF
(2)AF=AE
(3)证明:
∵四边形ABCD是菱形
∴AB=AD
∴∠ADB=∠ABD
∵∠ABD+∠ABF=180°
∠ADB+∠ADE=180°
∴∠ABF=∠ADE
∵BF = DE
∴△ABF≌△ADE(SAS)
∴AF=AE
【解析】
试题分析:根据观察图形,应该是连接AF或者CF
(1)连结AF(或连结CF)
(2)猜想AF=AE(连结CF的,则猜想CF=AE)
(3)证明:(以AF=AE为例,其他证法参照得分)
∵四边形ABCD是菱形
∴AB=AD
∴∠ADB=∠ABD
∵∠ABD+∠ABF=180°
∠ADB+∠ADE=180°
∴∠ABF=∠ADE
∵BF = DE
∴△ABF≌△ADE(SAS)
∴AF=AE


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】(7分)某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分为10分):
方案1:所有评委所给分的平均数,
方案2:在所有评委所给分中,去掉一个最高分和一个最低分.然后再计算其余给分的l平均数.
方案3:所有评委所给分的中位效.
方案4:所有评委所给分的众数.
为了探究上述方案的合理性.先对某个同学的演讲成绩进行了统计实验.下面是这个同学的得分统计图:

(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适台作为这个同学演讲的最后得分,并给出该同学的最后得分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E. 
(1)求证:AC平分∠DAB;
(2)连接BE交AC于点F,若cos∠CAD= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一直径是 ![]() 米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则: 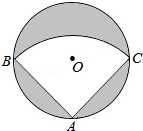
(1)AB的长为米;
(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=10,点C,D在线段AB上,且AC=DB=2;点P是线段CD上的动点,分别以AP,PB为边在线段AB的同侧作等边三角形AEP和等边三角形PFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,点G移动路径的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.甲工程队施工一天,需付工程款1万元;乙工程队施工一天,需付工程款0.6万元.根据甲、乙工程队的投标书测算,可有三种施工方案:
(A)甲队单独完成这项工程,刚好如期完成;
(B)乙队单独完成这项工程要比规定工期多用4天;
(C)若甲、乙两队合做3天后,剩下的工程由乙队单独做,也正好如期完工.
为了节省工程款,同时又能如期完工,你认为应选择哪一种方案?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料3600kg,乙种原料2410kg,计划利用这两种原料生产A,B两种产品共500件,产品每月均能全部售出.已知生产一件A产品需要甲原料9kg和乙原料3kg;生产一件B种产品需甲种原料4kg和乙种原料8kg.
(1)设生产x件A种产品,写出x应满足的不等式组.
(2)问一共有几种符合要求的生产方案?并列举出来.
(3)若有两种销售定价方案,第一种定价方案可使A产品每件获得利润1.15万元,B产品每件获得利润1.25万元;第二种定价方案可使A和B产品每件都获得利润1.2万元;在上述生产方案中哪种定价方案盈利最多?(请用数据说明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com