
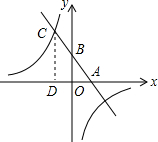
 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6.分析 (1)先求出A、B、C坐标,再利用待定系数法确定函数解析式.
(2)两个函数的解析式作为方程组,解方程组即可解决问题.
(3)根据图象一次函数的图象在反比例函数图象的下方,即可解决问题,注意等号.
解答 解:(1)∵OB=2OA=3OD=6,
∴OB=6,OA=3,OD=2,
∵CD⊥OA,
∴DC∥OB,
∴$\frac{OB}{CD}$=$\frac{AO}{AD}$,
∴$\frac{6}{CD}$=$\frac{3}{5}$,
∴CD=10,
∴点C坐标(-2,10),B(0,6),A(3,0),
∴$\left\{\begin{array}{l}{b=6}\\{3k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-2}\\{b=6}\end{array}\right.$,
∴一次函数为y=-2x+6.
∵反比例函数y=$\frac{n}{x}$经过点C(-2,10),
∴n=-20,
∴反比例函数解析式为y=-$\frac{20}{x}$.
(2)由$\left\{\begin{array}{l}{y=-2x+6}\\{y=-\frac{20}{x}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-2}\\{y=10}\end{array}\right.$或$\left\{\begin{array}{l}{x=5}\\{y=-4}\end{array}\right.$,
故另一个交点坐标为(5,-4).
(3)由图象可知kx+b≤$\frac{n}{x}$的解集:-2≤x<0或x≥5.
点评 本题考查一次函数与反比例函数的交点问题,解题的关键是学会利用待定系数法确定函数解析式,知道两个函数图象的交点坐标可以利用解方程组解决,学会利用图象确定自变量取值范围,属于中考常考题型.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
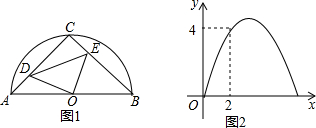
 如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
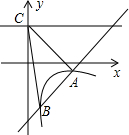 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(2,-1),B($\frac{1}{2}$,n)两点,直线y=2与y轴交于点C.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(2,-1),B($\frac{1}{2}$,n)两点,直线y=2与y轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com