
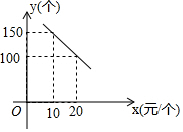
 某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示.
某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示.分析 (1)根据函数图象中两个点的坐标,利用待定系数法求解可得;
(2)根据“总利润=单件利润×销售量”列出函数解析,利用二次函数的性质可得最值情况;
(3)根据(2)中相等关系列出函数解析式,由二次函数的性质求解可得.
解答 解:(1)设y=kx+b,
根据函数图象可得:$\left\{\begin{array}{l}{10k+b=150}\\{20k+b=100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-5}\\{b=200}\end{array}\right.$,
∴y=-5x+200;
(2)设每天获利w元,
则w=(x-12)y=-5x2+260x-2400=-5(x-26)2+980,
∴当x=26时,w最大,最大利润为980元;
(3)设“十一”假期每天利润为P元,
则P=(0.8x-12)•y(1+200%)=-12x2+660x-7200=-12(x-$\frac{55}{2}$)2+1875,
∴当x=$\frac{55}{2}$时,P最大,
此时售价为0.8×$\frac{55}{2}$=22,
答:“十•一”假期该纪念品打八折后售价为22元.
点评 本题主要考查二次函数的应用和待定系数法求一次函数的解析式,熟练掌握销售问题中关于总利润的相等关系和二次函数的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
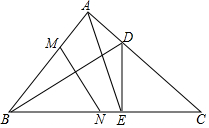 如图,△ABC中,∠BAC=90°,AB=AC,D为AC上一点,DE⊥BC于E,连接BD,M在AB上,AM=AD,MN⊥BD交BC于点N,若MN=5,AE=5$\sqrt{2}$,求BC的长.
如图,△ABC中,∠BAC=90°,AB=AC,D为AC上一点,DE⊥BC于E,连接BD,M在AB上,AM=AD,MN⊥BD交BC于点N,若MN=5,AE=5$\sqrt{2}$,求BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -2$\frac{3}{5}$ | D. | -$\frac{5}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
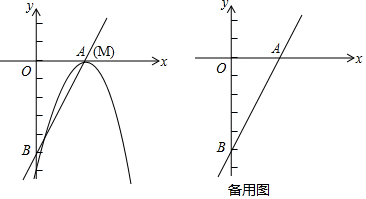
 如图,△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).
如图,△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图.在正方形ABCD中,点P是BC延长线上一点,BQ⊥PD于点Q,QN⊥BD于点N,连接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,则AN的长为$\sqrt{10}$.
如图.在正方形ABCD中,点P是BC延长线上一点,BQ⊥PD于点Q,QN⊥BD于点N,连接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,则AN的长为$\sqrt{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com