
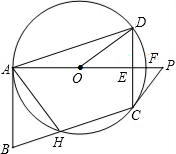
 如图,⊙O过?ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AP交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
如图,⊙O过?ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AP交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.分析 (1)要想证明△ABH是等腰三角形,只需要根据平行四边形的性质可得∠B=∠ADC,再根据圆内接四边形的对角互补,可得∠ADC+∠AHC=180°,再根据邻补角互补可知∠AHC+∠AHB=180°,从而可以得到∠ABH和∠AHB的关系,从而可以证明结论成立;
(2)要证直线PC是⊙O的切线,只需要连接OC,证明∠OCP=90°即可,根据平行四边形的性质和边AB与⊙O相切于点A,可以得到∠AEC的度数,又∠PCD=2∠DAF,∠DOF=2∠DAF,∠COE=∠DOF,通过转化可以得到∠OCP的度数,从而可以证明结论;
(3)根据题意和(1)(2)可以得到∠AED=90°,由平行四边形的性质和勾股定理,由AB=2,AD=$\sqrt{17}$,可以求得半径的长.
解答 (1)证明:∵四边形ADCH是圆内接四边形,
∴∠ADC+∠AHC=180°,
又∵∠AHC+∠AHB=180°,
∴∠ADC=∠AHB,
∵四边形ABCD是平行四边形,
∴∠ADC=∠B,
∴∠AHB=∠B,
∴AB=AH,
∴△ABH是等腰三角形;
(2)证明:连接OC,如右图所示,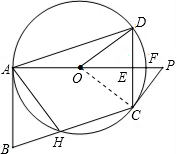
∵边AB与⊙O相切于点A,
∴BA⊥AF,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴CD⊥AF,
又∵FA经过圆心O,
∴$\widehat{DF}=\widehat{CF}$,∠OEC=90°,
∴∠COF=2∠DAF,
又∵∠PCD=2∠DAF,
∴∠COF=∠PCD,
∵∠COF+∠OCE=90°,
∴∠PCD+∠OCE=90°,
即∠OCP=90°,
∴直线PC是⊙O的切线;
(3)∵四边形ABCD是平行四边形,
∴DC=AB=2,
∵FA⊥CD,
∴DE=CE=1,
∵∠AED=90°,AD=$\sqrt{17}$,DE=1,
∴AE=$\sqrt{(\sqrt{17})^{2}-{1}^{2}}=\sqrt{17-1}=\sqrt{16}=4$,
设⊙O的半径为r,则OA=OD=r,OE=AE-OA=4-r,
∵∠OED=90°,DE=1,
∴r2=(4-r)2+12
解得,r=$\frac{17}{8}$,
即⊙O的半径是$\frac{17}{8}$.
点评 本题考查圆的综合题、平行四边形的性质、勾股定理、同弧所对的圆心角和圆周角的关系,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


科目:初中数学 来源: 题型:解答题
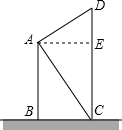 小华家与小丽家的两楼相邻,且相距10米,如图,小华家的楼高AB为18米;从小华家楼的顶部目测小丽家住的楼房CD的底部与顶部,视线与水平线的夹角分别为55°和35°,你能否求出小丽家住的楼房CD有多高?请说明理由.
小华家与小丽家的两楼相邻,且相距10米,如图,小华家的楼高AB为18米;从小华家楼的顶部目测小丽家住的楼房CD的底部与顶部,视线与水平线的夹角分别为55°和35°,你能否求出小丽家住的楼房CD有多高?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
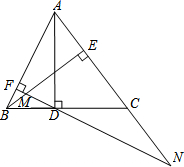 如图,AD、BE是△ABC的两条高,过点D作DF⊥AB,垂足为F,FD交BE于M,FD、AC的延长线交于点N.
如图,AD、BE是△ABC的两条高,过点D作DF⊥AB,垂足为F,FD交BE于M,FD、AC的延长线交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a3)2=a5 | B. | a3+a2=a5 | C. | a5÷a2=a3 | D. | ($\frac{x}{2}$)3=$\frac{{x}^{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
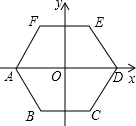 如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若D点的坐标为(2,0),则点F的坐标为( )
如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若D点的坐标为(2,0),则点F的坐标为( )| A. | (-1,$\sqrt{3}$) | B. | (-$\sqrt{3}$,1) | C. | (-$\sqrt{3}$,$\sqrt{3}$) | D. | (-1,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 居民(户) | 5 | 3 | 3 | 4 |
| 月用电量(度/户) | 30 | 42 | 50 | 51 |
| A. | 平均数是43.25 | B. | 众数是30 | C. | 方差是82.4 | D. | 中位数是42 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com