
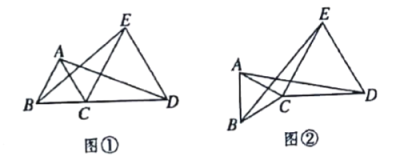
【题目】已知等边三角形的三条边相等,三个角都等于![]() ,如图,
,如图,![]() 与
与![]() 都是边三角形,连接
都是边三角形,连接![]() .
.
(1)如果点![]() 在同一条直线上,如图①所示,试说明:
在同一条直线上,如图①所示,试说明:![]() ;
;
(2)如果![]() 绕
绕![]() 点转过一个角度,如图②所示,(1)中的结论还能否成立?请说明理由.
点转过一个角度,如图②所示,(1)中的结论还能否成立?请说明理由.
科目:初中数学 来源: 题型:
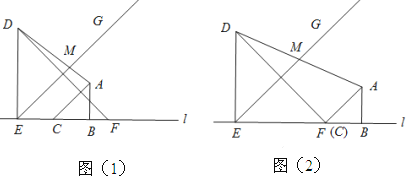
【题目】如图1,两个等腰直角三角板![]() 和
和![]() 有一条边在同一条直线
有一条边在同一条直线![]() 上,
上, ![]() ,
, ![]() .将射线
.将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,交直线
,交直线![]() 于点
于点![]() .将图1中的三角板
.将图1中的三角板![]() 沿直线
沿直线![]() 向右平移,设
向右平移,设![]() 、
、![]() 两点间的距离为
两点间的距离为![]() .
.
解答问题:
(1)①当点![]() 与点
与点![]() 重合时,如图2所示,可得
重合时,如图2所示,可得![]() 的值为 ;
的值为 ;
②在平移过程中, ![]() 的值为 (用含
的值为 (用含![]() 的代数式表示);
的代数式表示);
(2)将图2中的三角板![]() 绕点
绕点![]() 逆时针旋转,原题中的其他条件保持不变.当点
逆时针旋转,原题中的其他条件保持不变.当点![]() 落在线段
落在线段![]() 上时,如图3所示,计算
上时,如图3所示,计算![]() 的值;
的值;
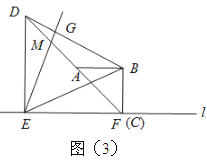
(3)将图1中的三角板ABC绕点C逆时针旋转![]() 度,
度, ![]() ≤
≤![]() ,原题中的其他条件保持不变.如图4所示,请补全图形,计算
,原题中的其他条件保持不变.如图4所示,请补全图形,计算![]() 的值(用含k的代数式表示).
的值(用含k的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB⊥BC,对角线AC、BD相交于点E,E为BD中点,且AD=BD,AB=2,∠BAC=30°,则DC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
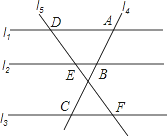
【题目】如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3 , 已知EF:DF=5:8,AC=24.
(1)求AB的长;
(2)当AD=4,BE=1时,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,做第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边做第三个菱形AB3C3D3,使∠B3=60°,依此类推,这样做的第2020个菱形ABnCnDn的边ADn的长是( ).

A.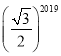 B.
B.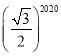 C.
C.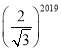 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:观察下面由※组成的图案和算式,解答问题:

1+3=22=4
1+3+5=32=9
1+3+5+7=42=16
1+3+5+7+9=52=25
(1)猜想1+3+5+7+9+…+29= = ;
(2)猜想1+3+5+7+9+…+(2n﹣1)+(2n+1)= = ;
(3)用上述规律计算:41+43+45+…+77+79.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张长方形纸板按图中虚线裁剪成![]() 块,其中有
块,其中有![]() 块是边长都为
块是边长都为![]() 厘米的大正方形,
厘米的大正方形,![]() 块是边长都为
块是边长都为![]() 厘米的小正方形,
厘米的小正方形,![]() 块是长为
块是长为![]() 厘米,宽为
厘米,宽为![]() 厘米的一模一样的小长方形,且
厘米的一模一样的小长方形,且![]() ,设图中所有裁剪线(虚线部分)长之和为
,设图中所有裁剪线(虚线部分)长之和为![]() 厘米.
厘米.

(1)![]() ______(试用
______(试用![]() ,
,![]() 的代数式表示);
的代数式表示);
(2)若每块小长方形的面积为![]() 平方厘米,四个正方形的面积和为
平方厘米,四个正方形的面积和为![]() 平方厘米,求
平方厘米,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用尺规作![]() 的平分线的方法如下:以
的平分线的方法如下:以![]() 为圆心,任意长为半径画弧交
为圆心,任意长为半径画弧交![]() ,
,![]() 于点
于点![]() ,
,![]() ,再分別以点
,再分別以点![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,作射线
,作射线![]() .由作法得
.由作法得![]() ,从而得两角相等.那么这两个三角形全等的根据是( )
,从而得两角相等.那么这两个三角形全等的根据是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况,随机抽取一部分学生进行问卷调查,统计整理并绘制了如图两幅不完整的统计图:
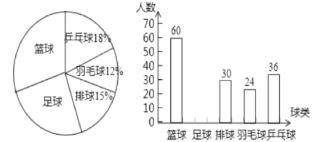
请根据以上统计图提供的信息,解答下列问题:
(1)共抽取___名学生进行问卷调查;
(2)补全条形统计图,求出扇形统计图中“篮球”所对应的圆心角的度数;
(3)该校共有2500名学生,请估计全校学生喜欢足球运动的人数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com