
分析 (1)首先对方程组进行化简即可求得含m的表示x和y得代数式;
(2)根据方程的解满足的解满足x≤0,y<0得到不等式组,解不等式组就可以得出m的范围,然后求得m的值;
(3)根据不等式2mx+x<2m+1的解为x>1,求出m的取值范围,即可解答.
解答 解:(1)$\left\{\begin{array}{l}{x+y=-m-7①}\\{x-y=3m+1②}\end{array}\right.$,
①+②得2x=2m-6,
所以,x=m-3;
①-②得2y=-4m-8,
所以,y=-2m-4,
故含m的代数式分别表示x和y为$\left\{\begin{array}{l}x=m-3\\ y=-2m-4\end{array}\right.$;
(2)∵x≤0,y<0
∴$\left\{\begin{array}{l}m-3≤0\\-2m-4<0\end{array}\right.$,
解,得-2<m≤3;
(3)(2m+1)x<2m+1,
∵原不等式的解集是x>1,
∴2m+1<0,
∴$m<-\frac{1}{2}$,
又∵-2<m≤3
∴$-2<m≤-\frac{1}{2}$,
∵m为整数,
∴m=-1.
点评 本题考查了解二元一次方程组和一元一次不等式,解决本题的关键是求出方程组的解集.


科目:初中数学 来源: 题型:解答题
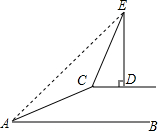 如图,某河大堤上有一颗大树ED,小明在A处测得树顶E的仰角为45°,然后沿坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,已知ED⊥CD,并且CD与水平地面AB平行,求大树ED的高度.(精确到1米)
如图,某河大堤上有一颗大树ED,小明在A处测得树顶E的仰角为45°,然后沿坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,已知ED⊥CD,并且CD与水平地面AB平行,求大树ED的高度.(精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com