
分析 因为此题点数较多,这就要求我们寻找规律,可以通过画图来寻找规律:通过画图发现,当点数为1时,三角形的个数为3;当点数为2时,三角形的个数为5;当点数为3时,三角形的个数为7,…,当点数为n时,三角形的个数为2n+1.依此即可求解.
解答 解:画图如下:
(1)图①中,当△ABC内只有1个点时,可分割成3个互不重叠的小三角形.
(2)图②中,当△ABC内只有2个点时,可分割成5个互不重叠的小三角形.
(3)图③中,当△ABC内只有3个点时,可分割成7个互不重叠的小三角形.
(4)根据以上规律,当△ABC内有n(n为正整数)个点时,可以把△ABC分割成(2n+1)个互不重叠的三角形.
因此三角形内部有2004个点,将三角形分割成互不重叠的三角形个数为:2n+1=2×2004+1=4009(个).
故m=4009.
故答案为:4009.
点评 此题考查了三角形边角关系,在解答探索规律问题时,至少应举出三个特例,寻找出规律后,按照此规律做题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
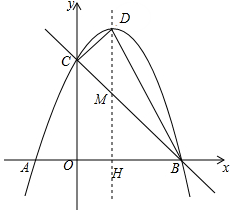 如图,已知抛物线y=-x2+bx+c轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC相交于点M,连接PB.
如图,已知抛物线y=-x2+bx+c轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC相交于点M,连接PB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
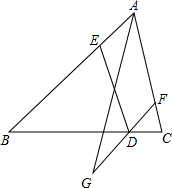 如图,在△ABC中,D,E,F分别为边BC,AB,AC上的点,ED∥AF且ED=AF,延长FD到点G,使DG=FD,求证:ED,AG互相平分.
如图,在△ABC中,D,E,F分别为边BC,AB,AC上的点,ED∥AF且ED=AF,延长FD到点G,使DG=FD,求证:ED,AG互相平分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
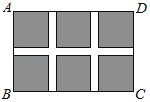 如图,某小区规划在一个长30m,宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,设通道的宽为xm.
如图,某小区规划在一个长30m,宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,设通道的宽为xm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,四边形OADC是矩形,OA=6,AB=4,直线y=-x+3与坐标轴交于D,E.设M是AB的中点,P是线段DE上的动点,
如图,在平面直角坐标系中,四边形OADC是矩形,OA=6,AB=4,直线y=-x+3与坐标轴交于D,E.设M是AB的中点,P是线段DE上的动点,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com