
【题目】若一条弧经过一个多边形相邻两边中点,并且该弧上所有点都在该多边形的内部或边上,则称该弧为此两边中点连线的EVA弧.例如,图1中,在△ABC中,D,E分别是△ABC两边的中点,如果![]() 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称![]() 为DE的一条EVA弧.
为DE的一条EVA弧.
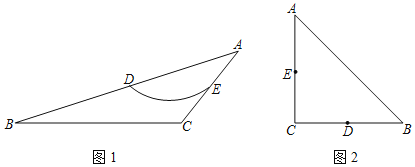
(1)如图2,在Rt△ABC中,∠C=90°,AC=BC=4![]() ,D,E分别是BC,AC的中点,画出DE的最长的EVA弧
,D,E分别是BC,AC的中点,画出DE的最长的EVA弧![]() ,并直接写出此时
,并直接写出此时![]() 的长;
的长;
(2)在平面直角坐标系中,已知点A(0,4),B(0,0),C(4t,0)(t>0),在△ABC中,D,E分别是AB,AC的中点.
①若t=1,求DE的EVA弧![]() 所在圆的圆心P的纵坐标m的取值范围;
所在圆的圆心P的纵坐标m的取值范围;
②若在△ABC中存在一条DE的EVA弧![]() ,使得
,使得![]() 所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
【答案】(1)图见解析,2π;(2)①m≤1或m≥2;②0<t≤2![]()
【解析】
(1)由三角函数值及等腰直角三角形性质可求得DE=4,最长中内弧即以DE为直径的半圆,弧DE的长即以DE为直径的圆周长的一半;
(2)根据三角形中内弧定义可知,圆心一定在DE的中垂线上,①当t=1时,要注意圆心P在DE上方的中垂线上均符合要求,在DE下方时必须AC与半径PE的夹角∠AEP满足90°≤∠AEP<135°;
②根据题意,t的最大值即圆心P在AC上时求得的t值,即可求解.
解:(1)如图2,以DE为直径画弧,
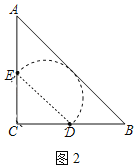
∵∠C=90°,AC=BC=4![]() ,
,
∴AB=8,
∵D,E分别是BC,AC的中点,
∴DE=![]() AB=4,
AB=4,
∵DE的最长的EVA弧![]() ,是以DE为直径的弧,
,是以DE为直径的弧,
∴![]() =
=![]() ×4π=2π;
×4π=2π;
(2)如图3,A(0,4),B(0,0),C(4t,0)(t>0),
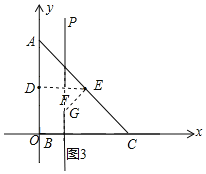
由垂径定理可知,圆心一定在线段DE的垂直平分线上,连接DE,作DE垂直平分线FP,作EG⊥AC交FP于G,
①当t=1时,C(4,0),
∴D(0,2),E(2,2),F(1,2),
若圆心在线段DE上方时,
设P(1,m)由三角形中内弧定义可知,圆心在线段DE上方射线FP上均可,
∴m≥2,
当圆心在线段DE下方时,
∵OA=OC,∠AOC=90°
∴∠ACO=45°,
∵DE∥OC
∴∠AED=∠ACO=45°
作EG⊥AC交直线FP于G,FG=EF=1,
根据三角形中内弧的定义可知,圆心在点G的下方(含点G)直线FP上时也符合要求;
∴m≤1,
综上所述,m≤1或m≥2.
②如图4,设圆心P在AC上,

∵P在DE中垂线上,
∴P为AE中点,作PM⊥OC于M,则PM=3,
∴P(t,3),
∵DE∥BC
∴∠ADE=∠AOB=90°
∴AE=![]() ,
,
∵PD=PE,
∴∠AED=∠PDE
∵∠AED+∠DAE=∠PDE+∠ADP=90°,
∴∠DAE=∠ADP
∴AP=PD=PE=![]() AE
AE
由三角形中内弧定义知,PD≤PM
∴![]() AE≤3,
AE≤3,
∴AE≤6,即![]() ≤6,
≤6,
解得:t≤![]() ,
,
∵t>0
∴0<t≤![]() .
.
如图5,设圆心P在BC上,则P(t,0)
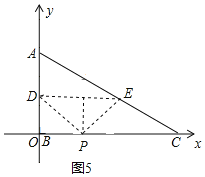
∴PD=PE=![]() ,
,
∵PC=3t,CE=![]() AC=
AC=![]() ,
,
由三角形中内弧定义知,∠PEC<90°,
∴PE2+CE2≥PC2
∴![]() ,
,
∵t>0
∴0<t≤![]() ;
;
综上所述,t的取值范围为:0<t≤![]() .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人同时骑自行车分别从A、B两地出发到AB之间的C地,且A、B、C三地在同一直线上.当乙到达C地时甲还未到达,乙在C地等了5分钟,接到甲的电话说他的自行车坏了需要工具修理,于是乙在C地拿了工具箱立即以原来![]() 倍的速度前往甲坏车处,乙与甲会合后帮助甲花了10分钟修好自行车,然后两人以甲原来
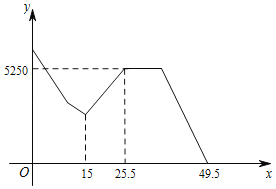
倍的速度前往甲坏车处,乙与甲会合后帮助甲花了10分钟修好自行车,然后两人以甲原来![]() 倍的速度骑行同时到达C地.甲乙两人距C地的距离之和y(米)与甲所用时间x(分钟)之间的函数关系如图所示(乙接电话和找工具箱的时间忽略不计),则A、B两地之间的距离为___米.
倍的速度骑行同时到达C地.甲乙两人距C地的距离之和y(米)与甲所用时间x(分钟)之间的函数关系如图所示(乙接电话和找工具箱的时间忽略不计),则A、B两地之间的距离为___米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=x+4与y=kx+4分别交x轴于点A、B,两直线交于y轴上同一点C,点D的坐标为(﹣![]() ,0),点E是AC的中点,连接OE交CD于点F.
,0),点E是AC的中点,连接OE交CD于点F.
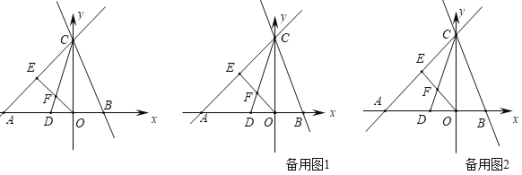
(1)求点F的坐标;
(2)若∠OCB=∠ACD,求k的值;
(3)在(2)的条件下,过点F作x轴的垂线1,点M是直线BC上的动点,点N是x轴上的动点,点P是直线l上的动点,使得以B,P,M、N为顶点的四边形是菱形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小元设计的“过圆上一点作圆的切线”的尺规作图过程.
已知:如图,⊙O及⊙O上一点P.
求作:过点P的⊙O的切线.


作法:如图,
①作射线OP;
②在直线OP外任取一点A,以点A为圆心,AP为半径作⊙A,与射线OP交于另一点B;
③连接并延长BA与⊙A交于点C;
④作直线PC;
则直线PC即为所求.
根据小元设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵ BC是⊙A的直径,
∴∠BPC=90°(____________)(填推理的依据).
∴OP⊥PC.
又∵OP是⊙O的半径,
∴PC是⊙O的切线(____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校今年学生节期间准备销售一种成本为每瓶4元的饮料.据去年学生节试销情况分析,按每瓶5元销售,一天能售出500瓶;在此基础上,销售单价每涨0.1元,该日销售量就减少10瓶.针对这种饮料的销售情况,请解答以下问题:
(1)设销售单价为每瓶x元,当日销售量为y元,求y与x的函数关系式(不写出x的取值范围);
(2)设该日销售利润为w元,求w与x的函数关系式(不写出x的取值范围);
(3)该日销售利润为800元,求销售单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交CD于点F,交AD的延长线于点E,若AB=4,BM=2,则△DEF的面积为( )

A.9B.8C.15D.14.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )

A. ![]() B.
B. ![]() C. 10D. 8
C. 10D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com