
分析 (1)顶点A在x轴上,对称轴是直线x=-2,则顶点坐标是(-2,0),利用待定系数法即可求得函数解析式;
(2)把(1,9)代入函数解析式作出判断即可;
(3)利用待定系数法求得一次函数的解析式,根据交点坐标即可确定当x取何值时,二次函数的函数值大于一次函数的函数值.
解答 解:(1)根据题意得函数的顶点坐标是(-2,0),
设函数的解析式是y=a(x+2)2,
把(0,4)代入得4=4a,
解得:a=1.
则函数的解析式是y=(x+2)2;
(2)当x=1时,(x+2)2=9,则M在函数图象上;
(3)设一次函数的解析式是y=kx+b,
根据题意得:$\left\{\begin{array}{l}{-2k+b=0}\\{b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=4}\end{array}\right.$.
则一次函数的解析式是y=2x+4.
当x<-2或x>0时,二次函数的函数值大于一次函数的函数值.
点评 本题考查了待定系数法求函数的解析式,以及函数值大小的比较,比较时要主要确定函数的交点坐标.


科目:初中数学 来源: 题型:选择题
| A. | 每个学生的体重是个体 | |
| B. | 40名学生的体重是一个样本 | |
| C. | 样本容量是5 | |
| D. | 全校八年级学生的体重的全体是总体 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
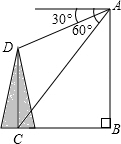 如图,在200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和60°,那么塔高是( )米.
如图,在200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和60°,那么塔高是( )米.| A. | $\frac{200}{3}$ | B. | $\frac{400}{3}$ | C. | $\frac{500}{3}$ | D. | $\frac{700}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
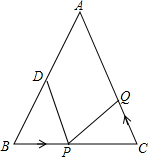 如图,在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
如图,在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 工资(元) | 3000 | 3200 | 3400 | 3600 |
| 人数(人) | 3 | 3 | 3 | 1 |
| A. | 3100元 | B. | 3200元 | C. | 3300元 | D. | 3400元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com