
现有一张矩形纸片,只用双手,不借助其他工具,你能将直角三等分吗?
小华是按以下步骤折叠的.
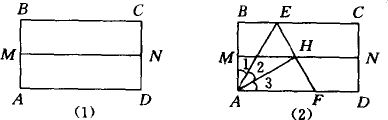
第一步:先把矩形对折,设折痕为MN,如图(1)所示;
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为H,得Rt△AHE;
第三步:沿EH线折叠,得折痕EF,如图(2)所示,此时,小华说“AE,AH就是∠BAD的三等分线”,你认为对吗?
若对,请证明这个结论;若不对,请说明理由.
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
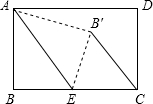 现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′.求线段B′C的长.
现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′.求线段B′C的长.查看答案和解析>>
科目:初中数学 来源: 题型:
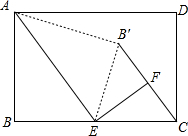 现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′,过E作EF垂直B′C,交B′C于F.
现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′,过E作EF垂直B′C,交B′C于F.查看答案和解析>>
科目:初中数学 来源: 题型:
 现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B'.则线段B'C=
现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B'.则线段B'C=查看答案和解析>>
科目:初中数学 来源: 题型:
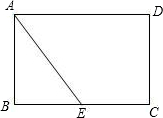 片沿直线AE折叠,使点B落在梯形AECD内,记为点B′.
片沿直线AE折叠,使点B落在梯形AECD内,记为点B′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com