
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]()
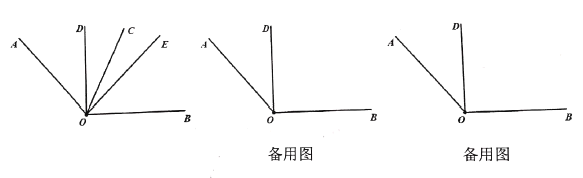
(1)求![]() ;
;
(2)![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转
的速度逆时针方向旋转![]() 秒(
秒(![]() ),
),![]() 为何值时
为何值时![]() ;
;
(3)射线![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转,射线
的速度逆时针方向旋转,射线![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度顺时针方向旋转,若射线
的速度顺时针方向旋转,若射线![]() 同时开始旋转
同时开始旋转![]() 秒(
秒(![]() )后得到
)后得到![]() ,求
,求![]() 的值.
的值.
【答案】(1)∠COE =20°;(2)当![]() =11时,
=11时,![]() ;(3)m=
;(3)m=![]() 或
或![]()
【解析】
(1)根据角平分线的定义和垂直定义即可求出∠BOD=90°,∠BOE=∠DOE =45°,即可求出∠AOB,再根据角平分线的定义即可求出∠BOC,从而求出∠COE;
(2)先分别求出OC与OD重合时、OE与OD重合时和OC与OA重合时运动时间,再根据t的取值范围分类讨论,分别画出对应的图形,根据等量关系列出方程求出t即可;
(3)先分别求出OE与OB重合时、OC与OA重合时、OC为OA的反向延长线时运动时、OE为OB的反向延长线时运动时间,再根据m的取值范围分类讨论,分别画出对应的图形,根据等量关系列出方程求出m即可;
解:(1)∵![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,
∴∠BOD=90°,∠BOE=∠DOE=![]() ∠BOD =45°
∠BOD =45°
∵![]()
∴∠AOB=∠AOE+∠BOE=130°
∵![]() 是
是![]() 的角平分线,
的角平分线,
∴∠AOC=∠BOC=![]() =65°
=65°
∴∠COE=∠BOC-∠BOE=20°
(2)由原图可知:∠COD=∠DOE-∠COE=25°,
故OC与OD重合时运动时间为25°÷5°=5s;OE与OD重合时运动时间为45°÷5°=9s;OC与OA重合时运动时间为65°÷5°=13s;
①当![]() 时,如下图所示
时,如下图所示
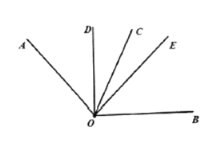
∵∠AOD=∠AOB-∠BOD=40°,∠COE=20°
∴∠AOD≠∠COE
∴∠AOD+∠COD≠∠COE+∠COD
∴此时![]() ;
;
②当![]() 时,如下图所示
时,如下图所示
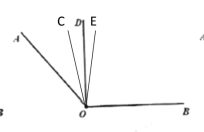
∵∠AOD=∠AOB-∠BOD=40°,∠COE=20°
∴∠AOD≠∠COE
∴∠AOD-∠COD≠∠COE-∠COD
∴此时![]() ;
;
③当![]() 时,如下图所示:
时,如下图所示:
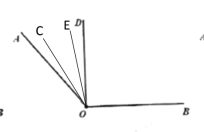
OC和OE旋转的角度均为5t
此时∠AOC=65°-5t,∠DOE=5t-45°
∵![]()
∴65-5t=5t-45
解得:t=11
综上所述:当![]() =11时,
=11时,![]() .
.
(3)OE与OB重合时运动时间为45°÷5°=9s;OC与OA重合时运动时间为65°÷10°=6.5s; OC为OA的反向延长线时运动时间为(180°+65°)÷10=24.5s;OE为OB的反向延长线时运动时间为(180°+45°)÷5=45s;
①当![]() ,如下图所示
,如下图所示
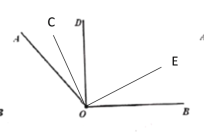
OC旋转的角度均为10m, OE旋转的角度均为5m
∴此时∠AOC=65°-10m,∠BOE=45°-5m
∵![]()
∴65-10m =![]() (45-5m)
(45-5m)
解得:m =![]() ;
;
②当![]() ,如下图所示
,如下图所示
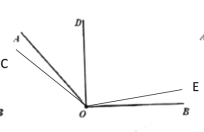
OC旋转的角度均为10m, OE旋转的角度均为5m
∴此时∠AOC=10m-65°,∠BOE=45°-5m
∵![]()
∴10m-65=![]() (45-5m)
(45-5m)
解得:m =![]() ;
;
③当![]() ,如下图所示
,如下图所示
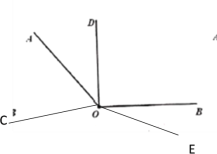
OC旋转的角度均为10m, OE旋转的角度均为5m
∴此时∠AOC=10m-65°,∠BOE=5m-45°
∵![]()
∴10m-65=![]() (5m-45)
(5m-45)
解得:m =![]() ,不符合前提条件,故舍去;
,不符合前提条件,故舍去;
综上所述:m=![]() 或
或![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
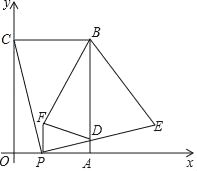
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(4,6),点P为线段OA上一动点(与点O、A不重合),连接CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点P作PF⊥OP且PF=PO(点F在第一象限),连结FD、BE、BF,设OP=t.
(1)直接写出点E的坐标(用含t的代数式表示):_____;
(2)四边形BFDE的面积记为S,当t为何值时,S有最小值,并求出最小值;
(3)△BDF能否是等腰直角三角形,若能,求出t;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两城相距800千米,一辆客车从甲城开往乙城,车速为![]() 千米/小时,同时一辆出租车比乙城开往甲城,车速为90千米/小时.
千米/小时,同时一辆出租车比乙城开往甲城,车速为90千米/小时.
(1)设客车行驶时间为![]() (小时),当
(小时),当![]() 时,客车与乙城的距离为_______千米(用含
时,客车与乙城的距离为_______千米(用含![]() 的代数式表示);
的代数式表示);
(2)已知![]() ,丙城在甲、乙两城之间,且与甲城相距260千米.
,丙城在甲、乙两城之间,且与甲城相距260千米.
①求客车与出租车相距200千米时客车的行驶时间;(列方程解答)
②已知客车和出租车在甲、乙之间的![]() 处相遇时,出租车乘客小李突然接到开会通知,需要立即返回,此时小李有两种返回乙城的方案;
处相遇时,出租车乘客小李突然接到开会通知,需要立即返回,此时小李有两种返回乙城的方案;
方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油的时间忽略不计;
方案二:在![]() 处换乘客车返回乙城.
处换乘客车返回乙城.
试通过计算,分析小李选择哪种方案能更快到达乙城?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别在x轴,y轴的正半轴上.点![]() 在线段EF上,过A作
在线段EF上,过A作![]() 分别交x轴,y轴于点B,C,点P为线段AE上任意一点(P不与A,E重合),连接CP,过E作
分别交x轴,y轴于点B,C,点P为线段AE上任意一点(P不与A,E重合),连接CP,过E作![]() ,交CP的延长线于点G,交CA的延长线于点D.有以下结论①
,交CP的延长线于点G,交CA的延长线于点D.有以下结论①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中正确的结论是_____.(写出所有正确结论的番号)
,其中正确的结论是_____.(写出所有正确结论的番号)

查看答案和解析>>
科目:初中数学 来源: 题型:
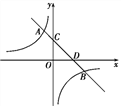
【题目】如图,反比例函数y=![]() 与一次函数y=k2x-k2+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=k2x-k2+2与坐标轴分别交于C,D两点,下列说法:①k1,k2<0;②点B的坐标为(3,-1);③当x<-1时,
与一次函数y=k2x-k2+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=k2x-k2+2与坐标轴分别交于C,D两点,下列说法:①k1,k2<0;②点B的坐标为(3,-1);③当x<-1时,![]() <k2x-k2+2;④tan∠OCD=-
<k2x-k2+2;④tan∠OCD=-![]() ,其中正确的是( )
,其中正确的是( )
A. ①③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,且点
,且点![]() 在点
在点![]() 的左侧,同时
的左侧,同时![]() 、
、![]() 满足
满足![]() ,
,![]() .
.
![]()
(1)由题意:![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)当点![]() 在数轴上运动时,点
在数轴上运动时,点![]() 到
到![]() 、
、![]() 两点距离之和的最小值为______.
两点距离之和的最小值为______.
(3)动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 沿数轴负方向匀速运动同时出发,点
沿数轴负方向匀速运动同时出发,点![]() 的速度是每秒
的速度是每秒![]() 个单位长度,点
个单位长度,点![]() 的速度是每秒2个单位长度,求运动几秒后,
的速度是每秒2个单位长度,求运动几秒后,![]() ?
?
(4)在数轴上找一点![]() ,使点
,使点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离之和等于10,请直接写出所有的点
三点的距离之和等于10,请直接写出所有的点![]() 对应的数.(不必说明理由)
对应的数.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
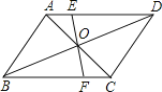
【题目】如图所示,线段EF过平行四边形ABCD的对角线的交点O,交AD于点E,交BC于点F。已知AB=4,BC=5,EF=3,那么四边形EFCD的周长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com