
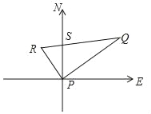
【题目】如图,某港口P位于东西方向的海岸线上,A、B两艘轮船同时从港口P出发,各自沿一固定方向航行,A轮船每小时航行12海里,B轮船每小时航行16海里.它们离开港口一个半小时后分别位于点R、Q处,且相距30海里.已知B轮船沿北偏东60°方向航行.
(1)A轮船沿哪个方向航行?请说明理由;
(2)请求出此时A轮船到海岸线的距离.
【答案】(1)A轮船沿北偏东30°方向航行;(2)此时A轮船到海岸线的距离为9![]() 海里.
海里.
【解析】
(1)根据题意得出RP=18海里,PQ=24海里,QR=30海里,利用勾股定理逆定理以及方向角得出答案;
(2)过点R作RM⊥PE于点M,然后利用sin60°=![]() ,得出答案.
,得出答案.
解:(1)由题意可得:RP=18海里,PQ=24海里,QR=30海里,
∵182+242=302,
∴△RPQ是直角三角形,
∴∠RPQ=90°,
∵B轮船沿北偏东60°方向航行,
∴∠RPS=30°,
∴A轮船沿北偏东30°方向航行;
(2)过点R作RM⊥PE于点M,则∠RPM=60°,
则sin60°=![]() ,
,
解得:RM=9![]() .
.
答:此时A轮船到海岸线的距离为9![]() 海里.
海里.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】世界上大部分国家都使用摄氏温度(℃),但美国,英国等国家的天气预报都使用华氏温度(℉),两种计量之间有如下对应:
摄氏温度(℃) | … | 0 | 10 | … |
华氏温度(℉) | … | 32 | 50 | … |
已知华氏温度y(℉)是摄氏温度x(℃)的一次函数.
求该一次函数的解析式;
当华氏温度14℉时,求其所对应的摄氏温度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6 ![]() ,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.
,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上. 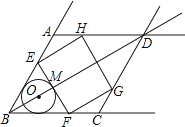
(1)求证:BO=2OM.
(2)设EF>HE,当矩形EFGH的面积为24 ![]() 时,求⊙O的半径.
时,求⊙O的半径.
(3)当HE或HG与⊙O相切时,求出所有满足条件的BO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个分别含有30°,45°角的一副直角三角板.
(1)如图1叠放在一起
若OC恰好平分∠AOB,则∠AOD= 度;
若∠AOC=40°,则∠BOD= 度;
(2)如图2叠放在一起,∠AOD=4∠BOC,试计算∠AOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线 ![]() (x>0)上的一个动点,PB⊥y轴于点B , 当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
(x>0)上的一个动点,PB⊥y轴于点B , 当点P的横坐标逐渐增大时,四边形OAPB的面积将会( ) 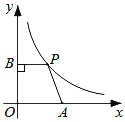
A.逐渐增大
B.不变
C.逐渐减小
D.先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.
(1)判断直线BE与线段AD之间的关系,并说明理由;
(2)若∠C=30°,图中是否存在等边三角形?若存在,请写出来并证明;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
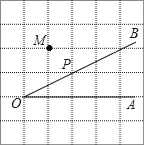
【题目】如图,点P是∠AOB的边OB上的一点.
(1)过点M画OB的平行线MN;
(2)过点P画OA的垂线,垂足为H;
(3)过点P画OB的垂线,交OA于点C:
则线段PH的长度是点P到 的距离, 是点C到直线OB的距离,因为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 .(用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=108°,OE是∠AOB的平分线,OC在∠AOE内.
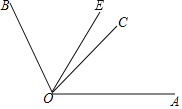
(1)若∠COE=![]() ∠AOE,求∠AOC的度数;
∠AOE,求∠AOC的度数;
(2)若∠BOC-∠AOC=72°,则OB与OC有怎样的位置关系?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com