
【题目】如图,正方形![]() 的对角线
的对角线![]() 和
和![]() 相交于点
相交于点![]() ,正方形
,正方形![]() 的边
的边![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
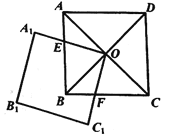
(1)求证:![]() ;
;
(2)如果正方形![]() 的边长为
的边长为![]() ,那么正方形
,那么正方形![]() 绕
绕![]() 点转动的过程中,与正方形
点转动的过程中,与正方形![]() 重叠部分的面积始终等于__________.(用含
重叠部分的面积始终等于__________.(用含![]() 的代数式表示)
的代数式表示)
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】设p,q都是实数,且p<q.我们规定:满足不等式p≤x≤q的实数x的所有取值的全体叫做闭区间,表示为[p,q].对于一个函数,如果它的自变量x与函数值y满足:当p≤x≤q时,有p≤y≤q,我们就称此函数是闭区间[p,q]上的“闭函数”.反比例函数y=![]() 是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山种了44棵苹果树.现在进入第三年收获期.收获时,先随意摘了5棵树上的苹果,称得每棵树摘得的苹果重量如下(单位:千克)35 35 34 39 37
(1)在这个问题中,总体指的是?个体指的是?样本是?样本容量是?
(2)试根据样本平均数去估计总体情况,你认为该农户可收获苹果大约多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有两条互相垂直的公路![]() ,A厂离公路
,A厂离公路![]() 的距离为2千米,离公路
的距离为2千米,离公路![]() 的距离为5千米;B厂离公路
的距离为5千米;B厂离公路![]() 的距离为11千米,离公路
的距离为11千米,离公路![]() 的距离为4千米;现在要在公路
的距离为4千米;现在要在公路![]() 上建造一仓库P,使A厂到P仓库的距离与B厂到P仓库的距离相等,求仓库P的位置.
上建造一仓库P,使A厂到P仓库的距离与B厂到P仓库的距离相等,求仓库P的位置.
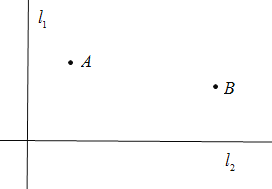
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题:
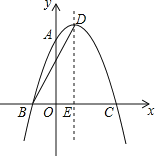
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
(3)点F在抛物线的对称轴上运动,是否存在点F,使△BFC的面积为4,如果存在,求出点F的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
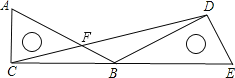
【题目】如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD.
(1)试判断△CBD的形状,并说明理由;
(2)求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用![]() 元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高
元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高![]() 元,商店用了
元,商店用了![]() 元,所购数量是第一次的
元,所购数量是第一次的![]() 倍.
倍.
(1)求第一批采购的书包的单价是多少元?
(2)若商店按售价为每个书包![]() 元,销售完这两批书包,总共获利多少元?
元,销售完这两批书包,总共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设![]() (分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为
(分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为![]() 千米,骑自行车学生骑行的路程为
千米,骑自行车学生骑行的路程为![]() 千米,
千米,![]() 关于
关于![]() 的函数图象如图所示.
的函数图象如图所示.
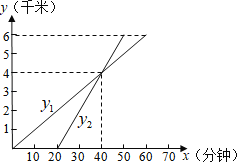
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元?
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com