
【题目】a 和5a大小比较是( )
A. a 小于5a
B. a 等于5a
C. a 大于5a
D.不能确定
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.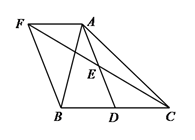
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:高斯上小学时,有一次数学老师让同学们计算“从1到100这100个正整数的和”.许多同学都采用了依次累加的计算方法,计算起来非常烦琐,且易出错.聪明的小高斯经过探索后,给出了下面漂亮的解答过程.
解:设S=1+2+3+…+100, ①
则S=100+99+98+…+1,②
①+②,得
2S=101+101+101+…+101.
(两式左右两端分别相加,左端等于2s,右端等于100个101的和)
所以2S=100x101,
S= ![]() ×100X101=5050 ③
×100X101=5050 ③
所以1+2+3+…+100=5050.
后来人们将小高斯的这种解答方法概括为“倒序相加法”.
请解答下面的问题:
(1)请你运用高斯的“倒序相加法”计算:1+2+3+…+200.
(2)请你认真观察上面解答过程中的③式及你运算过程中出现类似的③式,猜想:
1+2+3+…+n= .
(3)计算:101+102+103+…+2018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个样本的频数分布直方图中一共有4组,从左至右的组中值依次为5,8,11,14,频数依次为5,4,6,5,则频率为0.2的一组为( )
A.6.5~9.5
B.9.5~12.5
C.8~11
D.5~8
查看答案和解析>>
科目:初中数学 来源: 题型:
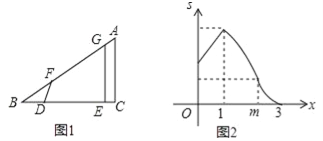
【题目】如图1,△ABC中,∠C=90°,线段DE在射线BC上,且DE=AC,线段DE沿射线BC运动,开始时,点D与点B重合,点D到达点C时运动停止,过点D作DF=DB,与射线BA相交于点F,过点E作BC的垂线,与射线BA相交于点G.设BD=x,四边形DEGF与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤m,1<x≤m,m<x≤3时,函数的解析式不同).
(1)填空:BC的长是 ;
(2)求S关于x的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线![]() 与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为( 、 ),BK的长是 ,CK的长是 ;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com