
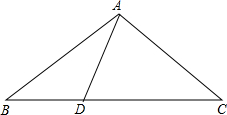
 如图,在△ABC中,∠B=40°,∠BAD=30°,若AB=CD,求∠ACD.
如图,在△ABC中,∠B=40°,∠BAD=30°,若AB=CD,求∠ACD. 分析 将△ABD沿AD所在直线对折,使点B落在点E的位置,得△AED,设AE与CD交于点O,根据全等三角形的性质得到∠DAE=∠BAD=30°,∠E=∠B=40°.由外角的性质得到∠AOC=∠BAD+∠B=70°,根据折叠的性质得到AE=AB,根据三角形的内角和即可得到结论.
解答 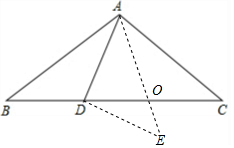 解:将△ABD沿AD所在直线对折,使点B落在点E的位置,得△AED,设AE与CD交于点O,
解:将△ABD沿AD所在直线对折,使点B落在点E的位置,得△AED,设AE与CD交于点O,
∵△AED≌△ABD,
∴∠DAE=∠BAD=30°,∠E=∠B=40°,
∵∠AOC为△ABO的一个外角,
∴∠AOC=2∠BAD+∠B=70°,
在△ADE中,∠EDO=180°-(∠1+∠2+∠4)=40°,
∴∠E=∠EDP,从而有OD=OE,
又∵AE为AB沿AD对折得到,有AE=AB,
∵AB=CD,∴CD=AE,
∴CD-OD=AE-OE,即OC=OA,
∴∠ACD=∠OAC,
在△ABC中,∠B+∠BAD+∠DAE+∠5+∠ACD=180°,
∴40°+30°+30°+∠ACD+∠ACD=108°,
∴∠ACD=40°.
点评 本题考查了等腰三角形的性质,三角形的外角的性质,三角形的内角和,折叠的性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
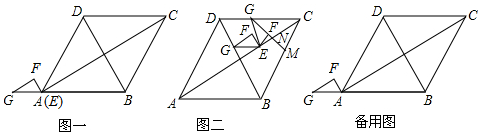
 如图,点E在正方形ABCD的对角线AC上,且EC=3AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为$\frac{9}{16}$a2.
如图,点E在正方形ABCD的对角线AC上,且EC=3AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为$\frac{9}{16}$a2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
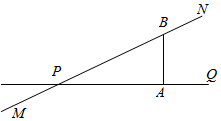 公路MN和公路PQ在点P处交汇,点A处有一所中学,PA=120米,AB=40$\sqrt{3}$米 且PA⊥AB.假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声影响?说明理由:如果受影响,已知设拖拉机速度为5米/秒,那么学校受影响的时间为多少秒?
公路MN和公路PQ在点P处交汇,点A处有一所中学,PA=120米,AB=40$\sqrt{3}$米 且PA⊥AB.假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声影响?说明理由:如果受影响,已知设拖拉机速度为5米/秒,那么学校受影响的时间为多少秒?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com