
如图1,抛物线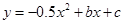 与x轴交于B(3,0)
、C(8.0)两点,抛物线另有一点A在第一象限内,连接AO、AC,且AO=AC.
与x轴交于B(3,0)
、C(8.0)两点,抛物线另有一点A在第一象限内,连接AO、AC,且AO=AC.
1.求抛物线的解析式;
2.将△OAC绕x轴旋转一周,求所得旋转体的表面积;
3.如图2,将△OAC沿x轴翻折后得△ODC,设垂直于x轴的直线l:x=n与(1)中所求的抛物线交于点M,与CD交于点N,若直线l 沿x轴方向左右平移,且交点M始终位于抛物线上A、C两点之间时,试探究:当n为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.

1.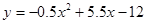 --------------4分(其中方程组正确2分)
--------------4分(其中方程组正确2分)
2.在图1中作AH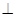 x轴于H, -----------------5分
x轴于H, -----------------5分
则OH=4, ------------------6分
当x=4时,y=2 所经A(4,2),OA=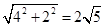 ----------7分
----------7分
表面积=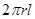 =
=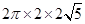 =
=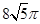 --------------------------8分
--------------------------8分
3.连接AD,交OC于E,----------------------------------9分
则OE=4,BE=OE-OB=1,EC=4
利用三角形相似(略)可得AE=2,所以DE=2, D(4,-2)
由C(8,0)、D(4,-2)得直线CD解析式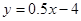 , --------10分
, --------10分
得N(n,0.5n-4)
由抛物线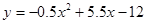 ,得M(
,得M(
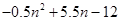 )
)
所以MN=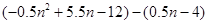 =
=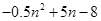 ------------11分
------------11分
四边形AMCN的面积=0.5MN×CE=0.5×(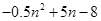 )×4
)×4
=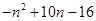 =
=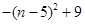
所以,当n=5时,四边形AMCN的面积取得最大值,这个最大值是9. -------12分
【解析】(1)把B、C两点坐标代入方程组得出二次函数的解析式;
(2)先用勾股定理求出OA长,然后利用表面积公式求解;
(3)先求出四边形面积的表达式,然后根据一元二次函数的性质求出面积最大值


科目:初中数学 来源: 题型:
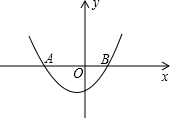 试问:是否存在实数k,使△AOC与△COB相似?若存在,求出相应的k的值;若不存在,请说明理由.
试问:是否存在实数k,使△AOC与△COB相似?若存在,求出相应的k的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
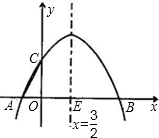 E,且OC=2,tan∠ACO=
E,且OC=2,tan∠ACO=| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
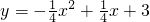 与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.
与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.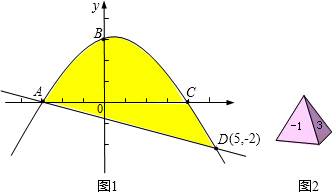
查看答案和解析>>
科目:初中数学 来源: 题型:
如图, 已知抛物线与x轴相交于A、B,点B的坐标为(10,0),顶点M的坐标为(4,8),点P从点M出发,以每秒1个单位的速度沿线段MA向A点运动;点Q从点A出发,以每秒2个单位的速度沿AB向B点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟。
(1)求抛物线的解析式;
(2)设△APQ的面积为S,求S与t之间的函数关系式,△APQ的面积是否有最大值?若有,请求出其最大值;若没有,请说明理由;
(3)当t为何值时,△APQ为等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com