
 如图,在梯形ABCD中,∠B=45°,∠C=60°,AD∥BC,AD=3,DC=6,求梯形的面积S.
如图,在梯形ABCD中,∠B=45°,∠C=60°,AD∥BC,AD=3,DC=6,求梯形的面积S. 分析 作AE⊥BC于E,DF⊥BC于F,则∠AEB=∠DFC=90°,AE=DF,AD=EF,求出∠CDF和∠BAE,再由三角函数求出CF、DF、BE、AE,由梯形的面积公式求出梯形ABCD的面积即可.
解答 解:作AE⊥BC于E,DF⊥BC于F,如图所示:
则四边形AEFD是矩形,
∴∠AEB=∠DFC=90°,AE=DF,AD=EF,
∴∠CDF=90°-∠C=30°,∠BAE=90°-∠B=45°,
∴CF=$\frac{1}{2}$DC=3,DF=$\sqrt{3}$CF=3$\sqrt{3}$,
∴BE=AE=DF=3$\sqrt{3}$,
∴BC=BE+EF+CF=3$\sqrt{3}$+6,
∴梯形ABCD的面积=$\frac{1}{2}$(AD+BC)×AE=$\frac{1}{2}$(3+3$\sqrt{3}$+6)×3$\sqrt{3}$=$\frac{27\sqrt{3}+27}{2}$.
点评 本题考查了梯形的性质、矩形的性质、三角函数、梯形面积的计算;熟练掌握梯形的性质,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:填空题
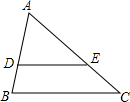 在△ABC中,点D在AB上,点E在AC上,且DE∥BC,$\frac{AD}{AB}$=$\frac{3}{4}$,则$\frac{EC}{AC}$=$\frac{1}{4}$.
在△ABC中,点D在AB上,点E在AC上,且DE∥BC,$\frac{AD}{AB}$=$\frac{3}{4}$,则$\frac{EC}{AC}$=$\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
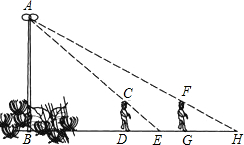 如图,花丛中一根灯杆AB上有一盏路灯A,灯光下,小明在D点处的影长DE=3米,沿BD方向走到点G,DG=5米,这时小明的影长GH=4米,如果小明的身高为1.7米,求路灯A离地面的高度.
如图,花丛中一根灯杆AB上有一盏路灯A,灯光下,小明在D点处的影长DE=3米,沿BD方向走到点G,DG=5米,这时小明的影长GH=4米,如果小明的身高为1.7米,求路灯A离地面的高度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{-0.064}$=-0.4 | B. | $\root{3}{(-2)^{3}}$=2 | C. | $\sqrt{(±2)^{2}}$=±2 | D. | (-$\sqrt{2}$)2+($\root{3}{2}$)3=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com