
【题目】近些年全国各地频发雾霾天气,给人民群众的身体健康带来了危害,某商场看到商机后决定购进甲、乙两种空气净化器进行销售.若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元,且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同.
(1)求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元?
(2)若该商场准备进货甲、乙两种空气净化器共30台,且进货花费不超过42000元,问最少进货甲种空气净化器多少台?
【答案】(1)每台甲种空气净化器、每台乙种空气净化器的进价分别为1200元,1500元(2)至少进货甲种空气净化器10台.
【解析】
(1)设每台甲种空气净化器为x元,乙种净化器为(x+300)元,根据用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同,列出方程求解即可;
(2)设甲种空气净化器为y台,乙种净化器为(30﹣y)台,根据进货花费不超过42000元,列出不等式求解即可.
(1)设每台甲种空气净化器为x元,乙种净化器为(x+300)元,由题意得:
![]() ,
,
解得:x=1200,
经检验得:x=1200是原方程的解,
则x+300=1500,
答:每台甲种空气净化器、每台乙种空气净化器的进价分别为1200元,1500元.
(2)设甲种空气净化器为y台,乙种净化器为(30﹣y)台,根据题意得:
1200y+1500(30﹣y)≤42000,
y≥10,
答:至少进货甲种空气净化器10台.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某超市每天能出售甲、乙两种肉集装箱共21箱,且甲集装箱3天的销售量与乙集装箱4天的销售量相同.
(1)求甲、乙两种肉类集装箱每天分别能出售多少箱?
(2)若甲种肉类集装箱的进价为每箱200元,乙种肉类集装箱的进价为每箱180元,现超市打算购买甲、乙两种肉类集装箱共100箱,且手头资金不到18080元,则该超市有几种购买方案?
(3)若甲种肉类集装箱的售价为每箱260元,乙种肉类集装箱的售价为每箱230元,在(2)的情况下,哪种方案获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
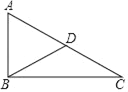
【题目】如图,在△ABC中,∠ABC=90°,BD为AC边上的中线.
(1)按如下要求尺规作图,保留作图痕迹,标注相应的字母:过点C作直线CE,使CE⊥BC于点C,交BD的延长线于点E,连接AE;
(2)求证:四边形ABCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
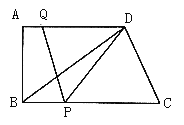
【题目】如图所示,在四边形ABCD中,AD//BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
(1)设△DPQ的面积为S,求S与t之间的函数关系式;
(2)分别求出出当t为何值时,①PD=PQ,②DQ=PQ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=45°,BD=2时,求D,F两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生课余生活,计划开设以下课外活动项目:A—版画,B—机器人,C—航模,D—园艺种植.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查(每位学生必须选且只能选一个项目),并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
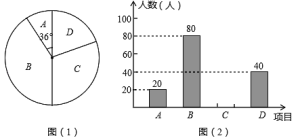
(1)这次被调查的学生共有 人;扇形统计图中,选“D—园艺种植”的学生人数所占圆心角的度数是 °
(2)请你将条形统计图补充完整;
(3)若该校学生总数为1000人,试估计该校学生中最喜欢“机器人”和最喜欢“航模”项目的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)~(2)题:
数学课上,老师出示了一道题:如图1,将一个直角三角板![]() 的直角边
的直角边![]() 摆放在直线
摆放在直线![]() 上,然后以直角顶点
上,然后以直角顶点![]() 为旋转中心顺时针旋转这个三角板.若射线
为旋转中心顺时针旋转这个三角板.若射线![]() 平分
平分![]() 、探究
、探究![]() 和
和![]() 的数量关系,并说明经过一段时间的思考后,同学们开始了交流:
的数量关系,并说明经过一段时间的思考后,同学们开始了交流:
小明:我根据老师的叙述画出图2,并计算出当![]() 时,
时,![]() 的度数是
的度数是![]() ;
;
小红:在小明的图形中,点![]() 、
、![]() 都在
都在![]() 的上方,我发现,在这种情况下,
的上方,我发现,在这种情况下,![]() 始终在
始终在![]() 的内部.若设
的内部.若设![]() 的度数是
的度数是![]() ,通过计算,
,通过计算,![]() 的度数可以用含
的度数可以用含![]() 的式子表示,得到
的式子表示,得到![]() 和
和![]() 的数量关系是
的数量关系是![]() ;
;
小华:我除了画小明的这种图形,还画了其余几种,也分别得出![]() 和
和![]() 的数量关系,从而解决了老师提出的问题.
的数量关系,从而解决了老师提出的问题.
老师:这些同学都先画出图形,再解决问题,这体现了图形的直性,但要注意一点,在初中阶段我们研究的角都是小于![]() 的.随着大家交流的深入,点
的.随着大家交流的深入,点![]() 的位置由
的位置由![]() 上方到直线
上方到直线![]() 外,
外,![]() 的值由数字到字母,这体现了从特殊到一般的思想,同学们再根据小华所说的进行探究,还能归纳出其他的数学思想方法!
的值由数字到字母,这体现了从特殊到一般的思想,同学们再根据小华所说的进行探究,还能归纳出其他的数学思想方法!
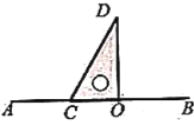
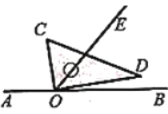
图1 图2
(1)如图2,点![]() 、
、![]() 都在
都在![]() 上方,
上方,![]() .
.
①用含![]() 的代数式表示
的代数式表示![]() 为_____________;
为_____________;
②小红的“![]() 始终在
始终在![]() 的内部”的说法是正确的吗,为什么?
的内部”的说法是正确的吗,为什么?
(2)根据小华的叙述,写出![]() 与
与![]() 的数量关系并说明.
的数量关系并说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,同时点
的速度移动,同时点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为
的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为![]() 秒,
秒,

![]() 求 秒后,
求 秒后, ![]() 的面积等于
的面积等于![]()
![]() 求 秒后,
求 秒后,![]() 的长度等于
的长度等于![]()
![]() 运动过程中,四边形APQC的面积能否等于
运动过程中,四边形APQC的面积能否等于![]() ?说明理由.
?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com