
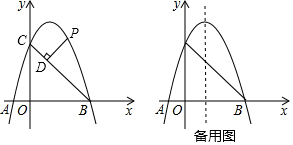
分析 (1)利用待定系数法求抛物线解析式;
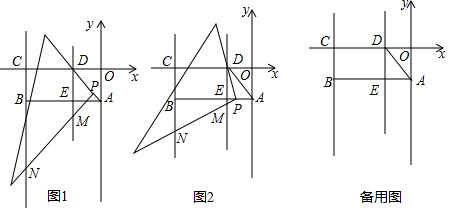
(2)①过P作PN⊥x轴于点N,交BC于点E,如图1,先利用待定系数法求出直线BC解析式为y=-x+3,设点P的坐标为(t,-t2+2t+3),则E(t,-t+3),所以PE=-t2+3t,再判定△PDE为等腰直角三角形得到PD=$\frac{{\sqrt{2}}}{2}$PE,所以PD=$\frac{{\sqrt{2}}}{2}$(-t2+3t),然后就利用二次函数的性质解决问题;
②过D作DG⊥x轴于点G,如图2,通过证明△BOC∽△BGD,利用相似比可求出DG=2,则点D的纵坐标为2,于是利用二次函数解析式可确定D点坐标,接着求出直线PD解析式为y=x+1,然后解方程组$\left\{\begin{array}{l}{y=x+1}\\{y=-{x}^{2}+2x+3}\end{array}\right.$可得到P点坐标,从而得到t的值;
(3)讨论:当四边形BQCM为平行四边形或四边形BCQM为平行四边形或四边形BCMQ为平行四边形,然后利用平行四边形的性质和点的平移坐标规律确定M点的横坐标,再利用二次函数解析式确定M点的纵坐.
解答 解:(1)设抛物线所对应的函数关系式为y=ax2+bx+c
将A(-1,0),B(3,0),C(0,3)代入y=ax2+bx+c得$\left\{\begin{array}{l}a-b+c=0\\ 9a+3b+c=0\\ c=3\end{array}\right.$,解得$\left\{\begin{array}{l}a=-1\\ b=2\\ c=3\end{array}\right.$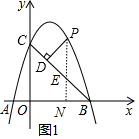
∴抛物线所对应的函数关系式为y=-x2+2x+3;
(2)①过P作PN⊥x轴于点N,交BC于点E,如图1,
设直线BC解析式为y=kx+b,
把B(3,0),C(0,3)代入y=kx+b得$\left\{\begin{array}{l}3k+b=0\\ b=3\end{array}\right.$,解得:k=-1,b=3,
∴直线BC解析式为y=-x+3,
设点P的坐标为(t,-t2+2t+3),则E(t,-t+3),
∴PE=-t2+2t+3-(-t+3)=-t2+3t,
∵OB=OC=3,
∴∠OBC=45°
∵PD⊥BC,
∴∠PED=45°,
∴△PDE为等腰直角三角形,
∴PD=$\frac{{\sqrt{2}}}{2}$PE=$\frac{{\sqrt{2}}}{2}$(-t2+3t)=-$\frac{{\sqrt{2}}}{2}$${(t-\frac{3}{2})^2}+$$\frac{{9\sqrt{2}}}{8}$,
∴当t=$\frac{3}{2}$时,PD的最大值为$\frac{{9\sqrt{2}}}{8}$;
②过D作DG⊥x轴于点G,如图2,则DG∥OC
∴△BOC∽△BGD,
∴$\frac{DG}{OC}=\frac{BD}{BC}$,
∵BD=2CD
∴BD:BC=2:3,
∴DG=$\frac{2}{3}$OC=2,
∴点D的纵坐标为2,
把y=2代入y=-x+3得x=1,
∴D点坐标为(1,2),
设直线PD解析式为y=x+b
把D(1,2)代入上式得2=1+b,解得b=1
∴直线PD解析式为y=x+1,
解方程组$\left\{\begin{array}{l}{y=x+1}\\{y=-{x}^{2}+2x+3}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$,
∴P(2,3),
即当BD=2CD时,t的值为2;
(3)当四边形BQCM为平行四边形时,点Q向左平移1个单位可得到C点,则点B向左平移1个单位得到M点,
即M点的横坐标为2,当x=2时,y=-x2+2x+3=3,此时M点的坐标为(2,3);
当四边形BCQM为平行四边形时,点C向右平移1个单位可得到Q点,则点B向右平移1个单位可得到M点,
即M点的横坐标为4,当x=4时,y=-x2+2x+3=-5,此时M点的坐标为(4,-5);
当四边形BCMQ为平行四边形时,点B向左平移2个单位可得到Q点,则点C向左平移2个单位得到M点,
即M点的横坐标为-1,当x=-2时,y=-x2+2x+3=-5,此时M点的坐标为(-2,-5),
综上所述,满足条件的M点的坐标为(2,3),(4,-5),(-2,-5).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的性质;会利用待定系数法求函数解析式;会利用相似比求线段的长;理解坐标与图形性质,掌握点的平移的坐标规律;会利用分类讨论的思想解决数学问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
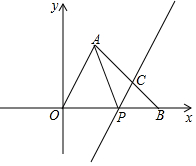 如图,将△OAB放在平面直角坐标系中,O为原点,点A(2,4),点B(6,0)在边OB上有一动点P,过P作PC∥OA交AB于C,连接AP.
如图,将△OAB放在平面直角坐标系中,O为原点,点A(2,4),点B(6,0)在边OB上有一动点P,过P作PC∥OA交AB于C,连接AP.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
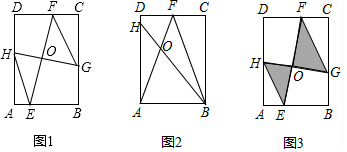
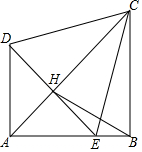 将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:
将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:| A. | 只有①② | B. | 只有③④ | C. | 只有①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AE∥BF,AC平分∠BAE,交BF于C.
如图,AE∥BF,AC平分∠BAE,交BF于C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=5米,AB=7米,∠MAD=45°,∠MBC=30°,求警示牌的高CD为多少米?(结果保留根号)
如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=5米,AB=7米,∠MAD=45°,∠MBC=30°,求警示牌的高CD为多少米?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com