
分析 (1)根据有理数的加法运算,可得答案;
(2)根据每次的绝对值,可得每次距A地的距离,根据有理数的大小比较,可得答案;
(3)根据行车的路程乘以单位耗油量,可得总耗油量.
解答 解:(1)-5+8-7+11+4-3-2=+6,
答:收工时在A地的东边,距A地6千米;
(2)第一次距A地|-5|=5(千米);
第二次:|-5+8|=3(千米);
第三次:|-5+8-7|=4(千米);
第四次:|-5+8-7+11|=7(千米);
第五次:|-5+8-7+11+4|=11(千米);
第六次:|-5+8-7+11+4-3|=8(千米);
第七次:|-5+8-7+11+4-3-2|=6(千米),
11>8>7>6>5>4>3.
故距A地最远的是第5次;
(3)|-5|+|+8|+|-7|+|+11|+|+4|+|-3|+|-2|=40(千米),
40×0.8=32(升).
答:从出发到收工共耗油32升.
点评 本题考查了正数和负数,利用了有理数的加法运算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
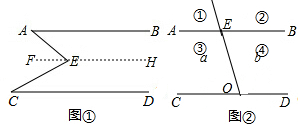 (1)如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,EC.探究∠AEC,∠EAB,∠ECD之间的关系.
(1)如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,EC.探究∠AEC,∠EAB,∠ECD之间的关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com