
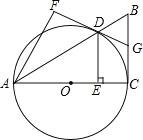
【题目】如图,已知Rt△ABC中,∠ACB=90°,以AC为直径的圆O交斜边AB于D.过D作DE⊥AC于E,将△ADE沿直线AB翻折得到△ADF.
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为10,sin∠FAD=![]() ,延长FD交BC于G,求BG的长.
,延长FD交BC于G,求BG的长.
【答案】(1)见解析(2)![]()
【解析】
(1)由△ADE沿直线AB翻折得到△ADF,得到∠DAE=∠DAF,∠AED=∠F=90°,由于OA=OD,于是得到∠DAE=∠ODA,根据平行线的判定定理得到OD∥AF,根据平行线的性质得到OD⊥DF,于是得到结论;
(2)连接DC,由于AC是 O的直径,即CD⊥AB;又FD与BC均是 O的切线且相交于点G由切线长定理可得:GD=GC,于是得到∠GDC=∠GCD,由于GD是Rt△BDC斜边上的中线,即GD=![]() BC,由于△ADE沿直线AB翻折得到△ADF,得到sin∠DAE=sin∠DAF=
BC,由于△ADE沿直线AB翻折得到△ADF,得到sin∠DAE=sin∠DAF=![]() ,解直角三角形得到sin∠DAC=
,解直角三角形得到sin∠DAC=![]() =
=![]() =
=![]() ,得DC=6,由勾股定理得AD=8;根据三角形相似即可得到结论.
,得DC=6,由勾股定理得AD=8;根据三角形相似即可得到结论.
(1)证明:
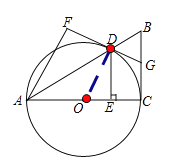
∵△ADE沿直线AB翻折得到△ADF,
∴∠DAE=∠DAF,∠AED=∠F=90°,
又∵OA=OD,
∴∠DAE=∠ODA,
∴∠DAF=∠ODA,
∴OD∥AF,
∴∠ODF+∠F=180°,
∴∠ODF=90°,
∴OD⊥DF,
∴DF是O的切线;
(2)连接DC,
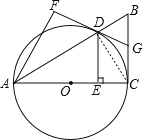
∵AC是圆O的直径,
∴∠ADC=90°,即CD⊥AB;
又∵FD与BC均是圆O的切线且相交于点G,
由切线长定理可得:GD=GC,
∴∠GDC=∠GCD,
又∵Rt△BDC中,∠GCD+∠B=90°,∠GDC+∠GDB=90°,
∴∠B=∠GDB,
∴GD=GB,
∴GD是Rt△BDC斜边上的中线,即GD=![]() BC,
BC,
∵△ADE沿直线AB翻折得到△ADF,
∴∠DAE=∠DAF,
∴sin∠DAE=sin∠DAF=![]() ,
,
又∵圆O的半径为5,
∴AC=10,
Rt△DAC中,∠ADC=90°,
∴sin∠DAC=DCAC=DC10=![]() ,得DC=6,
,得DC=6,
由勾股定理得AD=8;
在Rt△ADC与Rt△ACB中,∠ADC=∠ACB=90°,∠DAC=∠BAC,
∴Rt△ADC∽Rt△ACB,
∴![]() ,即
,即![]() ,解得BC=
,解得BC=![]() ;
;
∴GB=GD=![]() BC=
BC=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
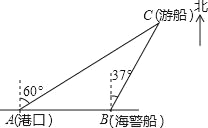
A. ![]() B.
B. ![]() C. sin37°D. cos37°
C. sin37°D. cos37°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() )的图象
)的图象![]() 经过点
经过点![]() (4,1),直线
(4,1),直线![]() 与图象
与图象![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)横、纵坐标都是整数的点叫做整点.记图象![]() 在点
在点![]() ,
,![]() 之间的部分与线段
之间的部分与线段![]() ,
,![]() ,
,![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内恰有4个整点,结合函数图象,求
内恰有4个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
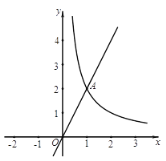
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与函数
与函数![]() 的图象交于点A(1,2).
的图象交于点A(1,2).
(1)求![]() 的值;
的值;
(2)过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,直线
,直线![]() 与直线l交于点B,与函数
与直线l交于点B,与函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点D.
轴交于点D.
①当点C是线段BD的中点时,求![]() 的值;
的值;
②当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
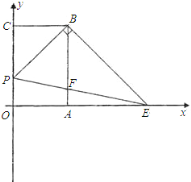
【题目】如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒.在运动的过程中,写出以P、O、E为顶点的三角形与△ABE相似时t的值为_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
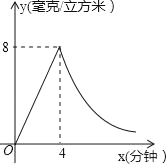
【题目】为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)成正比例,药物燃尽后,y与x成反比例(如图所示).已知药物点燃后4分钟燃尽,此时室内每立方米空气中含药量为8毫克.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)研究表明,当空气中每立方米的含药量不低于2毫克时,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() 、
、![]() .
.![]() 是线段
是线段![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .过点
.过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/18/2206393160556544/2207286529548288/STEM/a9696d0cbdac438aa94c80bfc838afd4.png]
(1)求该抛物线的解析式;
(2)试求线段![]() 的长
的长![]() 关于点
关于点![]() 的横坐标
的横坐标![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:

(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
(3)小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,且AB =6,C是⊙O上一点,D是![]() 的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.

(l)求证:AF⊥EF;
(2)填空:
①当BE= 时,点C是AF的中点;
②当BE= 时,四边形OBDC是菱形,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com