
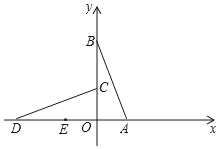
【题目】如图,已知点A(1,0),B(0,3),将△AOB绕点O逆时针旋转90°,得到△COD,设E为AD的中点.
(1)若F为CD上一动点,求出当△DEF与△COD相似时点F的坐标;
(2)过E作x轴的垂线l,在直线l上是否存在一点Q,使∠CQO=∠CDO?若存在,求出Q点的坐标;若不存在,请说明理由.
【答案】(1)F(﹣1,![]() )或F(﹣
)或F(﹣![]() ,
,![]() );(2)Q(﹣1,2)或(﹣1,﹣1).
);(2)Q(﹣1,2)或(﹣1,﹣1).
【解析】
(1)当△DEF∽△COD时,![]() ,DF=DEcos∠CDO=
,DF=DEcos∠CDO=![]() ,据此求出EF的长度和点F的坐标即可;
,据此求出EF的长度和点F的坐标即可;
(2)首先以CD为直径作圆,设其圆心为P,交直线a于点Q、Q′,连接PQ,P Q′,由圆周角定理,可得∠CQO=∠CQ′O=∠CDO,在Rt△CDO中,由勾股定理可得CD=![]() ,则PQ=
,则PQ=![]() CD=
CD=![]() ;然后求出点P的坐标是多少;设Q(﹣1,a),则(
;然后求出点P的坐标是多少;设Q(﹣1,a),则(![]() )2+(a﹣
)2+(a﹣![]() )2=
)2=![]() ,据此求出a的值是多少,进而求出Q点坐标是多少即可.
,据此求出a的值是多少,进而求出Q点坐标是多少即可.
(1)∵A(1,0),B(0,3),
∴OA=1,OB=3,
∵将△AOB绕点O逆时针旋转90°,得到△COD,
∴OC=1,OD=3,
∴C(0,1),D(﹣3,0),
如图1,当△DEF∽△COD时,![]() ,
,
∴EF=![]() ,
,
∴F(﹣1,![]() );
);
当△DEF∽△COD时,DF=DEcos∠CDO=![]() ,
,
作FK⊥OD于K,
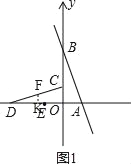
则FK=DFsin∠CDO=![]() ,DK=DFcos∠CDO=
,DK=DFcos∠CDO=![]() ,
,
∴F(﹣![]() ,
,![]() );
);
(2)如图2,以CD为直径作圆,设其圆心为P,交直线a于点Q、Q′,连接PQ,P Q′,

由圆周角定理,
可得∠CQO=∠CQ′O=∠CDO,
在Rt△CDO中,由勾股定理可得CD=![]() ,
,
则PQ=![]() CD=
CD=![]() ,
,
又∵P为CD中点,P(﹣![]() ,
,![]() ),
),
设Q(﹣1,a),
则(![]() )2+(a﹣
)2+(a﹣![]() )2=
)2=![]() ,
,
解得a=2或﹣1,
∴Q(﹣1,2)或(﹣1,﹣1).


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
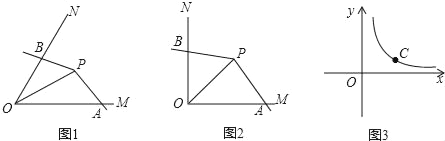
【题目】如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OAOB=OP2,我们就把∠APB叫做∠MON的智慧角.
(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°.求证:∠APB是∠MON的智慧角.
(2)如图1,已知∠MON=α(0°<α<90°),OP=2.若∠APB是∠MON的智慧角,连结AB,用含α的式子分别表示∠APB的度数和△AOB的面积.
(3)如图3,C是函数y=![]() (x>0)图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
(x>0)图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H.点G在⊙O上,过点G作直线EF,交CD延长线于点E,交AB的延长线于点F.连接AG交CD于K,且KE=GE.

(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若AC∥EF,![]() ,FB=1,求⊙O的半径.
,FB=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,网格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向下平移5格后得到△A1B1C1,写出点A1,B1,C1的坐标,并画出△A1B1C1;
(2)把△ABC绕点O按顺时针方向旋转180°后得到△A2B2C2,写出点A2,B2,C2的坐标,并画出△A2B2C2;
(3)把△ABC以点O为位似中心放大得到△A3B3C3,使放大前后对应线段的比为1∶2,写出点A3,B3,C3的坐标,并画出△A3B3C3.
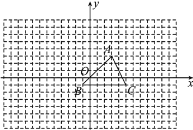
查看答案和解析>>
科目:初中数学 来源: 题型:
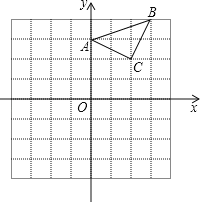
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5![]() 的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1
的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1![]() 污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元:
污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元:
(1)求出y与x的函数关系式.(纯利润=总收入-总支出)
(2)当y=106000时,求该厂在这个月中生产产品的件数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(-2,0),点B(0,4),点E在OB上,且∠OAE=∠OBA.
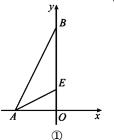
(1)如图①,求点E的坐标
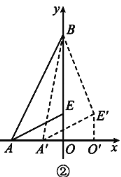
(2)如图②,将△AEO沿x轴向右平移得到△A′E′O′,连接A′B,BE′.
①设AA′=m,其中0<m<2,试用含m的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值时点E′的坐标;
②当A′B+BE′取得最小值时,求点E′的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com