
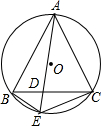
 如图,已知△ABC为⊙O的内接三角形,AB=AC=5,AD=4,则DE的长为$\frac{9}{4}$.
如图,已知△ABC为⊙O的内接三角形,AB=AC=5,AD=4,则DE的长为$\frac{9}{4}$. 分析 由已知条件和圆周角定理易证△ABD∽△AEB,由相似三角形的性质:对应边的比值相等可得AB,AD,AE的之间的数量关系,结合图形可得AE=AD+DE,进而可求出DE的长.
解答 解:
∵AB=AC=5,
∴∠ABD=∠ACB,
∵∠ACB=∠AEB,
∴∠ABD=∠AEB,
∵∠BAE=∠BAE,
∴△ABD∽△AEB,
∴$\frac{AB}{AD}=\frac{AE}{AB}$,
即AB2=AD•AE,
∵AD=4,AE=AD+DE,
∴52=4•(4+DE),
解得DE=$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题主要考查了三角形外接圆与外心的有关性质,用到的知识点有等腰三角形的性质、圆周角定理以及相似三角形的判定与性质,能够判定△ABD∽△AEB是解题的关键.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{15}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,用连线的方法,在图中按要求作图(保留作图痕迹,不写作法),在AB边上求一点N,连接CN,使CN=AM,并说明理由.
如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,用连线的方法,在图中按要求作图(保留作图痕迹,不写作法),在AB边上求一点N,连接CN,使CN=AM,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
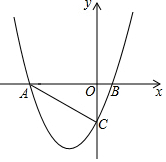 如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.
如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b | B. | -$\frac{1}{2}$a<-$\frac{1}{2}$b | C. | 2a+3>2b+3 | D. | -7a>-7b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com