
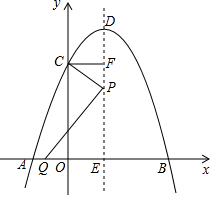 ČēĶ¼£¬Å×ĪļĻßy=-x2+bx+c¾¹żA£Ø-1£¬0£©£¬C£Ø0£¬3£©Į½µć£¬µćBŹĒÅ×ĪļĻßÓėxÖįĮķŅ»øö½»µć£¬Å×ĪļĻߵĶŌ³ĘÖįDE½»Å×ĪļĻßÓŚµćD£¬½»xÖįÓŚµćE£¬µćPŌŚÖ±ĻßDEÉĻ£¬¹żC×÷CF”ĶDE£¬“¹×ćĪŖµćF£¬Į¬½ÓCP£¬¹żµćP×÷PQ”ĶCP£¬½»xÖįÓŚµćQ£®ÉčµćPµÄׯ×ų±źĪŖm£®
ČēĶ¼£¬Å×ĪļĻßy=-x2+bx+c¾¹żA£Ø-1£¬0£©£¬C£Ø0£¬3£©Į½µć£¬µćBŹĒÅ×ĪļĻßÓėxÖįĮķŅ»øö½»µć£¬Å×ĪļĻߵĶŌ³ĘÖįDE½»Å×ĪļĻßÓŚµćD£¬½»xÖįÓŚµćE£¬µćPŌŚÖ±ĻßDEÉĻ£¬¹żC×÷CF”ĶDE£¬“¹×ćĪŖµćF£¬Į¬½ÓCP£¬¹żµćP×÷PQ”ĶCP£¬½»xÖįÓŚµćQ£®ÉčµćPµÄׯ×ų±źĪŖm£®·ÖĪö £Ø1£©ÓĆ“ż¶ØĻµŹż·Ø¼“æɽā¾öĪŹĢā£®
£Ø2£©·ÖČżÖÖĒéŠĪ£®ÓÉ”÷PCF”×”÷QPE£¬µĆµ½$\frac{CF}{PE}$=$\frac{PF}{QE}$£¬ĮŠ³ö·½³Ģ¼“æɽā¾öĪŹĢā£®
£Ø3£©ČēĶ¼4ÖŠ£¬µ±QÓėAÖŲŗĻŹ±£¬ÓÉ”÷PCF”×”÷QPE£¬µĆµ½$\frac{CF}{PE}$=$\frac{PF}{QE}$£¬æɵĆ$\frac{1}{m}$=$\frac{3-m}{2}$£¬½ā·½³Ģ¼“æɽā¾öĪŹĢā£®
£Ø4£©µ±PE=CF=1Ź±£¬”÷PCF”Õ”÷QPE£¬ÓÉ“Ė¼“æɽā¾öĪŹĢā£®
½ā“š ½ā£ŗ£Ø1£©°ŃA£Ø-1£¬0£©£¬C£Ø0£¬3£©“śČėy=-x2+bx+cµĆµ½$\left\{\begin{array}{l}{c=3}\\{-1-b+c=0}\end{array}\right.$£¬
½āµĆ$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=-x2+2x+3£®
£Ø2£©¢ŁČēĶ¼1ÖŠ£¬Ņ×ÖŖF£Ø1£¬3£©£¬E£Ø1£¬0£©£®
µ±0£¼m£¼3Ź±£¬ÓÉ”÷PCF”×”÷QPE£¬µĆµ½$\frac{CF}{PE}$=$\frac{PF}{QE}$£¬
”ą$\frac{1}{m}$=$\frac{3-m}{QE}$£¬
”ąQE=m£Ø3-m£©£®
¢ŚČēĶ¼2ÖŠ£¬µ±m”Ü0Ź±£¬ÓÉ”÷PCF”×”÷QPE£¬µĆµ½$\frac{CF}{PE}$=$\frac{PF}{QE}$£¬
”ą$\frac{1}{-m}$=$\frac{3-m}{QE}$£¬
”ąQE=m£Øm-3£©£¬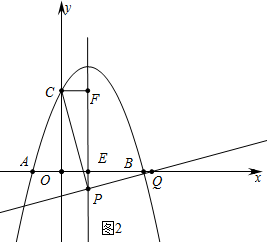
¢ŪČēĶ¼3ÖŠ£¬µ±m”Ż3Ź±£¬ÓÉ”÷PCF”×”÷QPE£¬µĆµ½$\frac{CF}{PE}$=$\frac{PF}{QE}$£¬
”ą$\frac{1}{m}$=$\frac{m-3}{QE}$£¬
”ąEQ=m£Øm-3£©£¬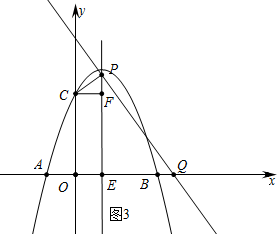
×ŪÉĻĖłŹö£¬EQ=$\left\{\begin{array}{l}{m£Øm-3£©}&{£Øm”Ż3£©}\\{m£Ø3-m£©}&{£Ø0£¼m£¼3£©}\\{m£Øm-3£©}&{£Øm”Ü0£©}\end{array}\right.$£®
£Ø3£©ČēĶ¼4ÖŠ£¬µ±QÓėAÖŲŗĻŹ±£¬ÓÉ”÷PCF”×”÷QPE£¬µĆµ½$\frac{CF}{PE}$=$\frac{PF}{QE}$£¬
”ą$\frac{1}{m}$=$\frac{3-m}{2}$£¬
½āµĆm=1»ņ2£®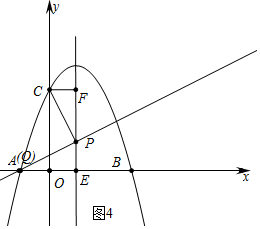
£Ø4£©µ±PE=CF=1Ź±£¬”÷PCF”Õ”÷QPE£¬
ÓÉ£Ø2£©æÉÖŖm=”Ą1Ź±£¬PE=CF£®
”ąm=”Ą1Ź±£¬”÷PCF”Õ”÷QPE£®
µćĘĄ ±¾Ģā漲鶞“ĪŗÆŹż×ŪŗĻĢā”¢“ż¶ØĻµŹż·Ø”¢ĻąĖĘČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢Č«µČČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒĮé»īÓ¦ÓĆĖłŃ§ÖŖŹ¶½ā¾öĪŹĢā£¬ŹĒÓĆ·ÖĄąĢÖĀŪµÄĖ¼ĻėĖ¼æ¼ĪŹĢā£¬ŹōÓŚÖŠæ¼Ń¹ÖįĢā£®


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
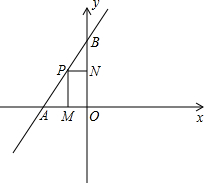 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļßy=$\frac{3}{2}$x+6ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£¬PĪŖĻ߶ĪABÉĻŅ»¶Æµć£Ø²»ÓėA£¬BĮ½µćÖŲŗĻ£©£¬¹żµćP×÷PM”ĶxÖį£¬PN”ĶyÖį£¬“¹×ć·Ö±šĪŖM£¬N£®ÉčOM=a£¬ĖıߊĪPMONĆ껿ĪŖs£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļßy=$\frac{3}{2}$x+6ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£¬PĪŖĻ߶ĪABÉĻŅ»¶Æµć£Ø²»ÓėA£¬BĮ½µćÖŲŗĻ£©£¬¹żµćP×÷PM”ĶxÖį£¬PN”ĶyÖį£¬“¹×ć·Ö±šĪŖM£¬N£®ÉčOM=a£¬ĖıߊĪPMONĆ껿ĪŖs£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬ABĪŖ”ŃOµÄÖ±¾¶£¬CDÓė”ŃOĻąĒŠÓŚµćC£¬ĒŅOD”ĶBC£¬“¹×ćĪŖF£¬OD½»”ŃOÓŚµćE£®
ČēĶ¼£¬ABĪŖ”ŃOµÄÖ±¾¶£¬CDÓė”ŃOĻąĒŠÓŚµćC£¬ĒŅOD”ĶBC£¬“¹×ćĪŖF£¬OD½»”ŃOÓŚµćE£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
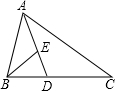 ČēĶ¼£¬”÷ABCÖŠ£¬D”¢EĮ½µć·Ö±šŌŚBC”¢ADÉĻ£¬ĒŅADĘ½·Ö”ĻBAC£¬Čō”ĻABE=”ĻC£¬AD£ŗED=3£ŗ1£¬Ōņ”÷BDEÓė”÷ADCµÄĆ껿±ČĪŖ£Ø””””£©
ČēĶ¼£¬”÷ABCÖŠ£¬D”¢EĮ½µć·Ö±šŌŚBC”¢ADÉĻ£¬ĒŅADĘ½·Ö”ĻBAC£¬Čō”ĻABE=”ĻC£¬AD£ŗED=3£ŗ1£¬Ōņ”÷BDEÓė”÷ADCµÄĆ껿±ČĪŖ£Ø””””£©| A£® | 16£ŗ45 | B£® | 2£ŗ9 | C£® | 1£ŗ9 | D£® | 1£ŗ3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 £Ø1£©ĪŅĆĒÖŖµĄ£¬½«Ņ»ĢõĻ߶ĪAB·Öøī³É“óŠ”Į½ĢõĻ߶ĪAP”¢PB£¬Ź¹AP£¾PB£¬µćP°ŃĻ߶ĪAB·Ö³ÉĮ½ĢõĻ߶ĪAPŗĶBP£¬ĒŅ$\frac{AP}{AB}$=$\frac{BP}{AP}$£¬µćP¾ĶŹĒĻ߶ĪABµÄ»Ę½š·Öøīµć£¬“ĖŹ±$\frac{PA}{AB}$µÄÖµĪŖ$\frac{\sqrt{5}-1}{2}$ £ØĢīŅ»øöŹµŹż£©£ŗ
£Ø1£©ĪŅĆĒÖŖµĄ£¬½«Ņ»ĢõĻ߶ĪAB·Öøī³É“óŠ”Į½ĢõĻ߶ĪAP”¢PB£¬Ź¹AP£¾PB£¬µćP°ŃĻ߶ĪAB·Ö³ÉĮ½ĢõĻ߶ĪAPŗĶBP£¬ĒŅ$\frac{AP}{AB}$=$\frac{BP}{AP}$£¬µćP¾ĶŹĒĻ߶ĪABµÄ»Ę½š·Öøīµć£¬“ĖŹ±$\frac{PA}{AB}$µÄÖµĪŖ$\frac{\sqrt{5}-1}{2}$ £ØĢīŅ»øöŹµŹż£©£ŗ²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com