
【题目】联想三角形外心的概念,我们可引入如下概念。
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心。
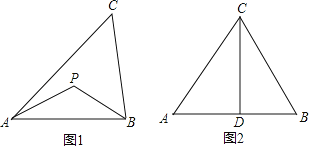
举例:如图1,若PA=PB,则点P为△ABC的准外心。
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=![]() AB,求∠APB的度数。
AB,求∠APB的度数。
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长。
【答案】∠APB=90°,PA=2或![]()
【解析】解:应用:①若PB=PC,连接PB,
则∠PCB=∠PBC,
∵CD为等边三角形的高,∴AD=BD,∠PCB=30°。
∴∠PBD=∠PBC=30°,∴PD=![]() DB=
DB=![]() AB。
AB。
与已知PD=![]() AB矛盾,∴PB≠PC。
AB矛盾,∴PB≠PC。
②若PA=PC,连接PA,同理可得PA≠PC。
③若PA=PB,由PD=![]() AB,得PD=AD =BD,∴∠APD=∠BPD=45°。∴∠APB=90°。
AB,得PD=AD =BD,∴∠APD=∠BPD=45°。∴∠APB=90°。
探究:∵BC=5,AB=3,∴AC=![]() 。
。
①若PB=PC,设PA=![]() ,则
,则![]() ,∴
,∴![]() ,即PA=
,即PA=![]() 。
。
②若PA=PC,则PA=2。
③若PA=PB,由图知,
在Rt△PAB中,不可能。
∴PA=2或![]() 。
。
应用:连接PA、PB,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况利用等边三角形的性质求出PD与AB的关系,然后判断出只有情况③是合适的,再根据等腰直角三角形的性质求出∠APB=45°,然后即可求出∠APB的度数。
探究:先根据勾股定理求出AC的长度,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况,根据三角形的性质计算即可得解


科目:初中数学 来源: 题型:
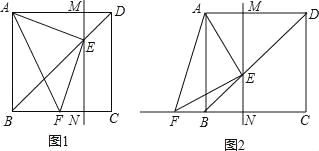
【题目】如图,点 E 是边长为 1 的正方形 ABCD 的对角线 BD 上的一个动点(不与 B、D 两点重合),过点 E 作直线 MN∥DC,交 AD 于 M,交 BC 于 N,连接 AE,作 EF⊥AE 于 E,交直线 CB 于 F.
(1)如图 1,当点 F 在线段 CB 上时,通过观察或测量,猜想△AEF 的形状,并证明你的猜想;
(2)如图 2,当点 F 在线段 CB 的延长线上时,其它条件不变,(1)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由;
(3)在点 E 从点D 向点B 的运动过程中,四边形 AFNM 的面积是否会发生变化?若发生了变化,请说明理由;若没有发生变化,请求出其面积的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】10月13日上午,2019“郑州银行杯”郑州国际马拉松赛在郑东新区CBD如意湖畔鸣枪开赛.今年的比赛共设置全程、半程马拉松和健康跑、家庭跑四个大项,吸引了来自全球32个国家和地区的2.6万名选手参加比赛在男子半程比赛中,中国选手刘洪亮起跑后,一直保持匀速前进,冲刺阶段突然加速,以1小时09分21秒的成绩获得男子半程冠军.下列能够反映刘洪亮在比赛途中速度v与时间t之间的函数关系的大致图象是( )
A.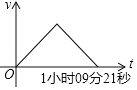 B.
B.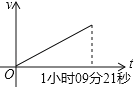
C.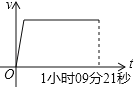 D.
D.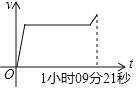
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示在三角形△ABC中AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,则下列四个结论中,①AB上一点与AC上一点到D的距离相等;②AD上任意一点到AB、AC的距离相等;③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的个数是
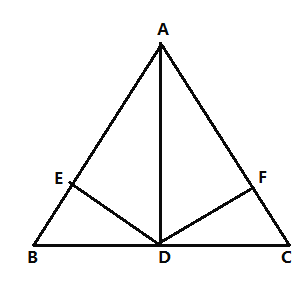
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
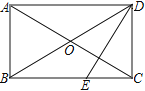
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1) 求证:四边形ABCD是矩形
(2) 若DE⊥AC交BC于E,∠ADB∶∠CDB=2∶3,则∠BDE的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,则下列五个结论中:①albic<0;②a﹣b+c>0;③2a﹣b<0;④abc<0;⑤4a+2b+c>0,错误的个数有( )
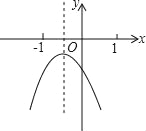
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com