
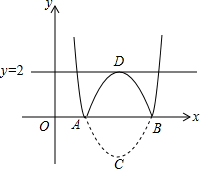
 ������y=x2+bx+c��x�ύ�ڵ�A��B������ΪC����������������x�����Ϸ��ۣ�ʹ��C���ڵ�D�����õ���ͼ��ʾͼ�μ���ͼ��F��
������y=x2+bx+c��x�ύ�ڵ�A��B������ΪC����������������x�����Ϸ��ۣ�ʹ��C���ڵ�D�����õ���ͼ��ʾͼ�μ���ͼ��F������ ��1�����������A��B�������꣬���ô���ϵ�������������ߵĽ���ʽ�����������C�����꼴�ɽ�����⣻
���ɢٿ�֪�����ۺ�������ߵĽ���ʽΪy=-x2+8x-7����ֱ��${l}_{1}��y=\frac{1}{2}x-6$ƽ�ƺ�Ľ���ʽy=$\frac{1}{2}$x+b����ֱ��y=$\frac{1}{2}$x+b����A��1��0��ʱ�����b��ֵ����ֱ��y=$\frac{1}{2}$x+b��y=-x2+8x-7ֻ��һ������ʱ�����b��ֵ���ɽ�����⣻
��2����ͼ2�У���ֱ��y=2��ͼ��F�����������㣬����������ֱ�ΪE��D��F����E��x1��y1����F��x2��y2������$\left\{\begin{array}{l}{y=2}\\{y={x}^{2}+bx+c}\end{array}\right.$��ȥy�õ�x2+bx+c-2=0���ɵ�x1+x2=-b��x1x2=c-2��������������y=x2+bx+c���Ķ����������Ϊ-2���ɵ�$\frac{4c-{b}^{2}}{4}$=-2����b2=4c+8����ֱ��l2��y=2��ͼ��F�������������ҹ�����ĺ�����Ϊһֱ�������ε����߳����ɵ�x22=x12+��$\frac{{x}_{1}+{x}_{2}}{2}$��2�����ø���ϵ����ϵ��ת��Ϊ����b��c�ķ��̼��ɽ�����⣻
��� �⣺��1���١�AB=6���Գ���x=4��
��A��1��0����B��7��0����
�������ߵĽ���ʽΪy=��x-1����x-7��=x2-8x+7=��x-4��2-9��
��C��4��-9����
��D��C����x��Գƣ�
��D��4��9����
��S��ABD=$\frac{1}{2}$��6��9=27��
����ͼ1�У�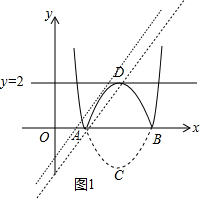
�ɢٿ�֪�����ۺ�������ߵĽ���ʽΪy=-x2+8x-7��
��ֱ��${l}_{1}��y=\frac{1}{2}x-6$ƽ�ƺ�Ľ���ʽy=$\frac{1}{2}$x+b��
��ֱ��y=$\frac{1}{2}$x+b����A��1��0��ʱ��0=$\frac{1}{2}$+b��
b=-$\frac{1}{2}$��
��ֱ��y=$\frac{1}{2}$x+b��y=-x2+8x-7ֻ��һ������ʱ��
��$\left\{\begin{array}{l}{y=\frac{1}{2}x+b}\\{y=-{x}^{2}+8x-7}\end{array}\right.$��ȥy�õ�x2-$\frac{15}{2}$x+b+7=0��
�ɡ�=0�ɵ�b=$\frac{113}{16}$��
��-$\frac{1}{2}$-��-6��=$\frac{11}{2}$��$\frac{113}{16}$-��-6��=$\frac{209}{16}$��
�۲�ͼ���֪����$\frac{11}{2}$��t��$\frac{209}{16}$ʱ����l1��ͼ��F���ĸ������㣮
��2����ͼ2�У���ֱ��y=2��ͼ��F�����������㣬����������ֱ�ΪE��D��F��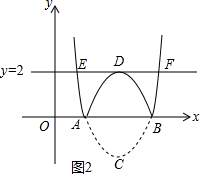
��E��x1��y1����F��x2��y2����
��$\left\{\begin{array}{l}{y=2}\\{y={x}^{2}+bx+c}\end{array}\right.$��ȥy�õ�x2+bx+c-2=0��
��x1+x2=-b��x1x2=c-2��
������������y=x2+bx+c���Ķ����������Ϊ-2��
��$\frac{4c-{b}^{2}}{4}$=-2��
��b2=4c+8��
��ֱ��l2��y=2��ͼ��F�������������ҹ�����ĺ�����Ϊһֱ�������ε����߳���
��x22=x12+��$\frac{{x}_{1}+{x}_{2}}{2}$��2��
�ࣨx2+x1����x2-x1��=$\frac{��{x}_{1}+{x}_{2}��^{2}}{4}$��
��16��x2-x1��2=��x1+x2��2��
��16[��x1+x2��2-4x1x2]=��x1+x2��2��
��16[b2-4��c-2��]=b2��
��16[4c+8-4c+8]=4c+8��
��c=62��b=-16��16��������Ϊb��0����
��b=-16��c=62��
���� ���⿼����κ����ۺ��⡢���۱任��ƽ�Ʊ任��һ�κ�����Ӧ�á�һԪ���η��̵ĸ���ϵ���Ĺ�ϵ����Ԫ���η������֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ò������������������⣬�����п�ѹ���⣮


 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д� ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
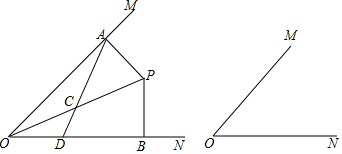
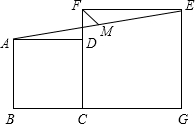 ��ͼ��������ABCD��������CGEF�ı߳��ֱ���3��5���ҵ�B��C��G��ͬһֱ���ϣ�M���߶�AE���е㣬����MF����MF�ij�Ϊ$\sqrt{2}$��
��ͼ��������ABCD��������CGEF�ı߳��ֱ���3��5���ҵ�B��C��G��ͬһֱ���ϣ�M���߶�AE���е㣬����MF����MF�ij�Ϊ$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ֱ������ϵ�У���֪��A��-3��0����B��0��4�����ԡ�OAB��������ת�任�����εõ���1����2����3����4�������2016��ֱ�����궥�������Ϊ��������
��ͼ����ֱ������ϵ�У���֪��A��-3��0����B��0��4�����ԡ�OAB��������ת�任�����εõ���1����2����3����4�������2016��ֱ�����궥�������Ϊ��������| A�� | ��8053��0�� | B�� | ��8064��0�� | C�� | ��8053��$\frac{12}{5}$�� | D�� | D����8064��$\frac{12}{5}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
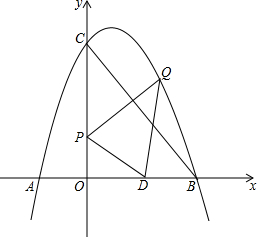 ��֪������y=$-\frac{1}{3}{x}^{2}+\frac{5}{3}x+12$��x�ύ�ڵ�A��B��A��B����ࣩ����y�ύ�ڵ�C������BC��y���ϵĵ�P��0��m��������P��BC�Ĵ��߽��Գ����Ҳ��������ڵ�Q��DΪx����һ���㣮
��֪������y=$-\frac{1}{3}{x}^{2}+\frac{5}{3}x+12$��x�ύ�ڵ�A��B��A��B����ࣩ����y�ύ�ڵ�C������BC��y���ϵĵ�P��0��m��������P��BC�Ĵ��߽��Գ����Ҳ��������ڵ�Q��DΪx����һ���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
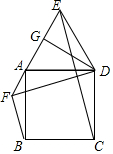 ��ͼ��������ABCD����A��ֱ��AE����D��DG��AE��AG=GE����DE��
��ͼ��������ABCD����A��ֱ��AE����D��DG��AE��AG=GE����DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3$\sqrt{3}$ | B�� | 6 | C�� | 2$\sqrt{3}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com