
| A. | 将油滴入水中,油会浮在水面上 | |
| B. | 车辆随机到达一个路口,遇到红灯 | |
| C. | 如果a2=b2,那么a=b | |
| D. | 掷一枚质地均匀的硬币,一定正面向上 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 调查你所在的班级同学的身高情况 | B. | 调查全国中学生心理健康现状 | ||
| C. | 调查我市食品合格情况 | D. | 调查中央电视台《少儿节目》收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
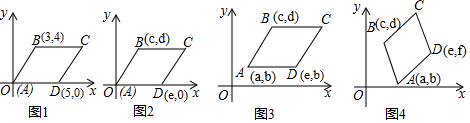
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.
在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
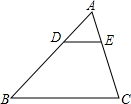 如图,在△ABC中,D、E分别为AB、AC上的点,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则$\frac{AD+DE+AE}{AB+BC+AC}$=$\frac{1}{3}$.
如图,在△ABC中,D、E分别为AB、AC上的点,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则$\frac{AD+DE+AE}{AB+BC+AC}$=$\frac{1}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com