练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
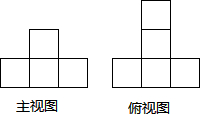
    20．用若干个大小相同的小正方形体组合成的几何体的主视图和俯视图如图所示，下面所给的四个选项中，不可能是这个几何体的左视图的是（　　）
    A．B．C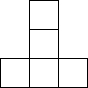．D．

    分析 由俯视图可得此几何体底面有5个小正方形分为3列3排，根据主视图可得这个几何体的左视图有2层高，依此即可求解．

    解答 解：由俯视图可得此几何体底面有5个小正方形分为3列3排，根据主视图可得这个几何体的左视图有2层高，
    可得这个几何体的左视图不可能是3层高．
    故选：C．

    点评 此题主要考查了画三视图，关键是根据主视图和俯视图分析出每排小正方体的个数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．如图1，在平面直角坐标系中，抛物线y=-$\frac{1}{3}$x2+$\frac{2\sqrt{3}}{3}$x+3与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，抛物线的顶点为点E．
    （1）判断△ABC的形状，并说明理由；
    （2）经过B，C两点的直线交抛物线的对称轴于点D，点P为直线BC上方抛物线上的一动点，当△PCD的面积最大时，Q从点P出发，先沿适当的路径运动到抛物线的对称轴上点M处，再沿垂直于抛物线对称轴的方向运动到y轴上的点N处，最后沿适当的路径运动到点A处停止．当点Q的运动路径最短时，求点N的坐标及点Q经过的最短路径的长；
    （3）如图2，平移抛物线，使抛物线的顶点E在射线AE上移动，点E平移后的对应点为点E′，点A的对应点为点A′，将△AOC绕点O顺时针旋转至△A1OC1的位置，点A，C的对应点分别为点A1，C1，且点A1恰好落在AC上，连接C1A′，C1E′，△A′C1E′是否能为等腰三角形？若能，请求出所有符合条件的点E′的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

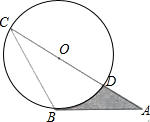    11．如图，AB是⊙O的切线，B为切点，AC经过点O，与⊙O分别相交于点D，C．若∠ACB=30°，AB=$\sqrt{3}$，则阴影部分的面积是（　　）
    A．$\frac{\sqrt{3}}{2}$B．$\frac{π}{6}$C．$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$D．$\frac{\sqrt{3}}{3}$-$\frac{π}{6}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．如图，∠AOB的一边OA为平面镜，∠AOB=37°36′，在OB上有一点E，从E点射出一束光线经OA上一点D反射，反射光线DC恰好与OB平行，则∠DEB的度数是（　　）
    A．75°36′B．75°12′C．74°36′D．74°12′

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

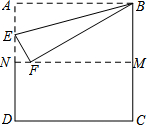    15．如图，把正方形纸片ABCD沿对边中点所在的直线对折后展开，折痕为MN，再过点B折叠纸片，使点A落在MN上的点F处，折痕为BE．若AB的长为2，则FM的长为（　　）
    A．2B．$\sqrt{3}$C．$\sqrt{2}$D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：（$\frac{x+8}{{x}^{2}-4}$-$\frac{2}{x-2}$）$÷\frac{x-4}{{x}^{2}-4x+4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．已知x1、x2是一元二次方程3x2=6-2x的两根，则x1-x1x2+x2的值是（　　）
    A．$-\frac{4}{3}$B．$\frac{8}{3}$C．$-\frac{8}{3}$D．$\frac{4}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：（-1）2016-（2-$\sqrt{3}$）0+$\sqrt{25}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．关于x的方程x2-4=0的根是（　　）
    A．2B．-2C．2，-2D．2，$\frac{1}{2}$

    查看答案和解析>>

    同步练习册答案