
【题目】(12分)(1)如图1,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,且MN=DM.设OM=a,请你利用基本活动经验直接写出点N的坐标_____(用含a的代数式表示);
(2)如果(1)的条件去掉“且MN=DM”,加上“交∠CBE的平分线与点N”,如图2,求证:MD=MN.如何突破这种定势,获得问题的解决,请你写出你的证明过程.
(3)如图3,请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,请你指出正确的结论,并给出证明.

【答案】(1)N(2+a,a);(2)见解析;(3)见解析.
【解析】 (1)如图1中,作NE⊥OB于E,只要证明△DMO≌△MNE,即可解决问题.
(2)如图2中,在OD上取OH=OM,连接HM,只要证明△DHM≌△MBN即可.
(3)结论:MN平分∠FMB成立.如图3中,在BO延长线上取OA=CF,过M作MP⊥DN于P,因为∠NMB+∠CDF=45°,所以只要证明∠FMN+∠CDF=45°即可解决问题.
解:(1)解:如图1中,作NE⊥OB于E,

∵∠DMN=90°,
∴∠DMO+∠NME=90°,∠NME+∠MNE=90°,
∴∠DMO=∠MNE,
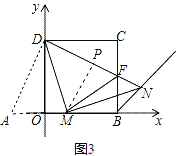
在△DMO和△MNE中,
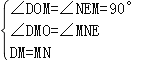 ,
,
∴△DMO≌△MNE,
∴ME=DO=2,NE=OM=a,
∴OE=OM+ME=2+a,
∴点N坐标(2+a,a),
故答案为N(2+a,a).
(2)证明:如图2中,在OD上取OH=OM,连接HM,

∵OD=OB,OH=OM,
∴HD=MB,∠OHM=∠OMH,
∴∠DHM=180°﹣45°=135°,
∵NB平分∠CBE,
∴∠NBE=45°,
∴∠NBM=180°﹣45°=135°,
∴∠DHM=∠NBM,
∵∠DMN=90°,
∴∠DMO+∠NMB=90°,
∵∠HDM+∠DMO=90°,
∴∠HDM=∠NMB,
在△DHM和△MBN中,
 ,
,
∴△DHM≌△MBN(ASA),
∴DM=MN.
(3)结论:MN平分∠FMB成立.
证明:如图3中,在BO延长线上取OA=CF,
在△AOD和△FCD中,
 ,
,
∴△DOA≌△DCF,
∴AD=DF,∠ADO=∠CDF,
∵∠MDN=45°,
∴∠CDF+∠ODM=45°,
∴∠ADO+∠ODM=45°,
∴∠ADM=∠FDM,
在△DMA和△DMF中,
 ,
,
∴△DMA≌△DMF,
∴∠DFM=∠DAM=∠DFC,
过M作MP⊥DN于P,则∠FMP=∠CDF,
由(2)可知∠NMF+∠FMP=∠PMN=45°,
∴∠NMB=∠MDH,∠MDO+∠CDF=45°,
∴∠NMB=∠NMF,即MN平分∠FMB.
“点睛”本题考查四边形综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质,解题的关键是学会添加辅助线,构造全等三角形,记住一些基本图形,可以使得我们在观察新问题的时候很迅速地联想,属于中考压轴题.


科目:初中数学 来源: 题型:
【题目】如图,在△ABO中,AB⊥OB,OB=![]() ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )

A.(-1,-![]() )
)
B.(-1,-![]() )或(-2,0)
)或(-2,0)
C.(-![]() ,1)或(0,﹣2)
,1)或(0,﹣2)
D.(-![]() ,1)
,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意抛掷一枚骰子两次,骰子停止转动后,计算朝上的点数的和.
(1)和最小的是多少,和最大的是多少?
(2)下列事件:①点数的和为7;②点数的和为1;③点数的和为15.哪些是不可能性事件?哪些是不确定事件?
(3)点数的和为7与点数的和为2的可能性谁大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元,每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若该商品每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?
(3)在(2)的条件下,每件商品的售价为多少元时,每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com