
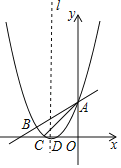
【题目】如图,抛物线y=![]() x2+bx+c与直线y=
x2+bx+c与直线y=![]() x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
(1)求抛物线的解析式;
(2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式是y=![]() x2+
x2+![]() x+3;(2)|MB﹣MD|取最大值为
x+3;(2)|MB﹣MD|取最大值为![]() ;(3)存在点P(1,6).
;(3)存在点P(1,6).
【解析】(1)根据待定系数法,可得函数解析式;
(2)根据对称性,可得MC=MD,根据解方程组,可得B点坐标,根据两边之差小于第三边,可得B,C,M共线,根据勾股定理,可得答案;
(3)根据等腰直角三角形的判定,可得∠BCE,∠ACO,根据相似三角形的判定与性质,可得关于x的方程,根据解方程,可得x,根据自变量与函数值的对应关系,可得答案.
(1)将A(0,3),C(﹣3,0)代入函数解析式,得
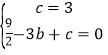 ,解得
,解得![]() ,
,
抛物线的解析式是y=![]() x2+
x2+![]() x+3;
x+3;
(2)由抛物线的对称性可知,点D与点C关于对称轴对称,
∴对l上任意一点有MD=MC,
联立方程组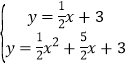 ,
,
解得![]() (不符合题意,舍),
(不符合题意,舍),![]() ,
,
∴B(﹣4,1),
当点B,C,M共线时,|MB﹣MD|取最大值,即为BC的长,
过点B作BE⊥x轴于点E,
 ,
,
在Rt△BEC中,由勾股定理,得
BC=![]() ,
,
|MB﹣MD|取最大值为![]() ;
;
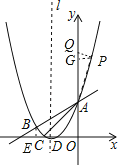
(3)存在点P使得以A,P,Q为顶点的三角形与△ABC相似,
在Rt△BEC中,∵BE=CE=1,
∴∠BCE=45°,
在Rt△ACO中,
∵AO=CO=3,
∴∠ACO=45°,
∴∠ACB=180°﹣45°﹣45°=90°,
过点P作PQ⊥y轴于Q点,∠PQA=90°,
设P点坐标为(x,![]() x2+
x2+![]() x+3)(x>0)
x+3)(x>0)
①当∠PAQ=∠BAC时,△PAQ∽△CAB,
∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,
∴△PGA∽△BCA,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
解得x1=1,x2=0(舍去),
∴P点的纵坐标为![]() ×12+
×12+![]() ×1+3=6,
×1+3=6,
∴P(1,6),
②当∠PAQ=∠ABC时,△PAQ∽△CBA,
∵∠PGA=∠ACB=90°,∠PAQ=∠ABC,
∴△PGA∽△ACB,
∴![]() ,
,
即![]() =3,
=3,
∴![]() ,
,
解得x1=﹣![]() (舍去),x2=0(舍去)
(舍去),x2=0(舍去)
∴此时无符合条件的点P,
综上所述,存在点P(1,6).


科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=![]() AB时,求t的值.
AB时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少万元?
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面有4张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,请在方格纸中分别画出符合要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:
(1)画一个直角边长为4,面积为6的直角三角形.
(2)画一个底边长为4,面积为8的等腰三角形.
(3)画一个面积为5的等腰直角三角形.
(4)画一个边长为2![]() ,面积为6的等腰三角形.
,面积为6的等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为______.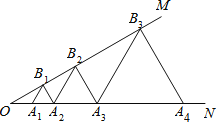
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,顶点A、C分别在x轴、y轴上,反比例函数y=![]() (k≠0,x>0)的图象与正方形OABC的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN,则下列选项中的结论错误的是( )
(k≠0,x>0)的图象与正方形OABC的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN,则下列选项中的结论错误的是( )
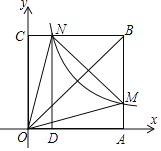
A. △ONC≌△OAM
B. 四边形DAMN与△OMN面积相等
C. ON=MN
D. 若∠MON=45°,MN=2,则点C的坐标为(0,![]() +1)
+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为线段AB上一点,在△ACM,△CBN中,AC=CM,BC=CN,∠ACM=∠BCN=60°,连接AN交CM于点E,连接BM交CN于点F.
求证:(1)AN=BM.(2)△CEF是等边三角形

查看答案和解析>>
科目:初中数学 来源: 题型:
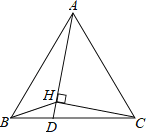
【题目】如图,△ABC是等边三角形,AB=![]() ,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,![]() 的三个顶点的位置如图所示,现将
的三个顶点的位置如图所示,现将![]() 沿
沿![]() 的方向平移,使得点
的方向平移,使得点![]() 移至图中的点
移至图中的点![]() 的位置.
的位置.
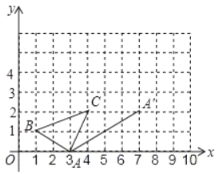
(1)在直角坐标系中,画出平移后所得![]() (其中
(其中![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的对应点).
的对应点).
(2)(1)中所得的点![]() ,
,![]() 的坐标分别是________,________.
的坐标分别是________,________.
(3)直接写出![]() 的面积为________.
的面积为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com