
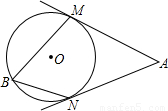
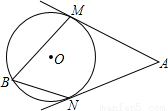
 16、如图,AM、AN分别切⊙O于M、N两点,点B在⊙O上,且∠MBN=70°,则∠A=
16、如图,AM、AN分别切⊙O于M、N两点,点B在⊙O上,且∠MBN=70°,则∠A= 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源:第35章《圆(二)》中考题集(09):35.3 探索切线的性质(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:第3章《圆》中考题集(32):3.2 点、直线与圆的位置关系,圆的切线(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2008年江苏省南京市栖霞区中考数学二模试卷(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2007年湖北省孝感市中考数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com