
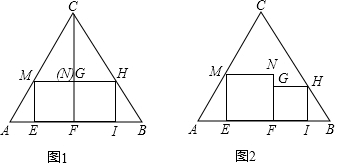
分析 (1)根据等边三角形的性质得到CF=$\frac{\sqrt{3}+1}{2}$,设两个正方形的边长为x,则MH=EI=2x,根据相似三角形的性质即可得到结论;
(2)设正方形MEFN的边长为x,正方形FIHG的边长为y,则AE=$\frac{\sqrt{3}}{3}$x,BI=$\frac{\sqrt{3}}{3}$y,列方程得到x+y=1,于是得到结论;
(3)根据不等式的性质即可得到结论.
解答 解:(1)∵点N和G重合,
∴EI=MH=2GF,CF⊥AB,
∵△ABC是等边三角形,AB=1+$\frac{\sqrt{3}}{3}$,
∴CF=$\frac{\sqrt{3}+1}{2}$,
设两个正方形的边长为x,则MH=EI=2x,
∵MH∥AB,
∴△CMH∽△CAB,
∴$\frac{MH}{AB}$=$\frac{CG}{CF}$,即$\frac{2x}{1+\frac{\sqrt{3}}{3}}$=$\frac{\frac{\sqrt{3}+1}{2}-x}{\frac{\sqrt{3}+1}{2}}$,
∴x=$\frac{1}{2}$,
∴EI=1;
(2)EI的长不发生改变,
理由:设正方形MEFN的边长为x,正方形FIHG的边长为y,
则AE=$\frac{\sqrt{3}}{3}$x,BI=$\frac{\sqrt{3}}{3}$y,
∴$\frac{\sqrt{3}}{3}$x+x+y+$\frac{\sqrt{3}}{3}$y=1+$\frac{\sqrt{3}}{3}$,
∴x+y=1,
∴EI=1,
即在两个正方形变化过程中,EI的长不发生改变;
(3)由(2)得x+y=1,则x2+y2≥$\frac{(x+y)^{2}}{2}$=$\frac{1}{2}$,当且仅当x=y=$\frac{1}{2}$时取等号,
∴这两个正方形面积和的最小值为$\frac{1}{2}$.
点评 本题考查了正方形的性质,等边三角形的性质,不等式的性质,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 3.0≤a≤3.2 | B. | 3.14≤a<3.15 | C. | 3.144≤a<3.149 | D. | 3.05≤a<3.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | sinA=$\frac{1}{2}$ | B. | cosA=$\frac{1}{2}$ | C. | tanA=$\frac{1}{2}$ | D. | cotA=$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com