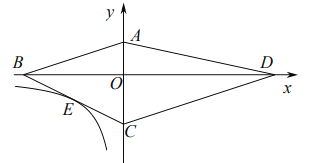
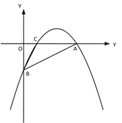
【题目】如图，四边形
的项点都在坐标轴上，若
与
面积分别为
和
，若双曲线
恰好经过
的中点
，则
的值为__________．
【答案】6
【解析】
根据AB//CD，得出△AOB与△OCD相似，利用△AOB与△OCD的面积分别为8和18，得：AO：OC=BO：OD=2：3，然后再利用同高三角形求得S△COB=12，设B、 C的坐标分别为（a，0）、（0，b），E点坐标为（
a，b）进行解答即可.
解：∵AB//CD，
∴△AOB∽△OCD，
又∵△ABD与△ACD的面积分别为8和18，
∴△ABD与△ACD的面积比为4：9，
∴AO：OC=BO：OD=2：3
∵S△AOB=8
∴S△COB=12
设B、 C的坐标分别为（a，0）、（0，b），E点坐标为（a，b）
则OB=| a | 、OC=| b |
∴|a|×|b|=12即|a|×|b|=24
∴|a|×|b|=6
又∵
，点E在第三象限
∴k=xy=a×b=6
故答案为6.
浙江名校名师金卷系列答案
全优冲刺100分系列答案科目：初中数学 来源： 题型：
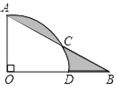
【题目】如图，∠AOB＝90°，∠B＝30°，以点O为圆心，OA为半径作弧交AB于点A、点C，交OB于点D，若OA＝3，则阴影都分的面积为___________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度
（单位：
）与足球被踢出后经过的时间
（单位：
）之间的关系如下表：
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论：①足球距离地面的最大高度为
；②足球飞行路线的对称轴是直线
；③足球被踢出
时落地；④足球被踢出
时，距离地面的高度是
.
其中正确结论的个数是（ ）
A．1 B．2 C．3 D．4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读以下材料：
材料一：如果两个两位数
和
将它们各自的十位数字和个位数字交换位置后得到两个完全不同的新数
，
，这两个两位数的乘积与交换后的两个两位数的乘积相等，则称这样的两个两位数为一对“有缘数对”．
例如：
，所以，46和96是一对“有缘数对”，
材料二：在进行一些数学式计算时，我们可以把某一单项式或多项式看作一个整体，运用整体换元，使得运算更简单．
例如：计算
，令：
，
原式
解决如下问题：
（1）①请任写一对“有缘数对”____________和____________．
②并探究“有缘数对”和，
，
，
，
之间满足怎样的等量关系．并写出证明过程．
（2）若两个两位数
与
是一对“有缘数对，请求出这两个两位数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】【题目】如图①，一次函数 y＝
x - 2 的图像交 x 轴于点 A，交 y 轴于点 B，二次函数 y＝
x2 bx c的图像经过 A、B 两点，与 x 轴交于另一点 C．
（1）求二次函数的关系式及点 C 的坐标；
（2）如图②，若点 P 是直线 AB 上方的抛物线上一点，过点 P 作 PD∥x 轴交 AB 于点 D，PE∥y 轴交 AB 于点 E，求 PD＋PE 的最大值；
（3）如图③，若点 M 在抛物线的对称轴上，且∠AMB＝∠ACB，求出所有满足条件的点 M的坐标．
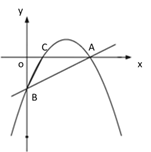
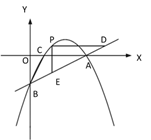
① ② ③
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了了解初三学生的中考体育备考情况，西安铁一中分校体育组从初三年级全年级学生中随机抽取部分学生进行测试，现将从报排球项目所有女生中随机抽取到的60名女生的排球成绩(40秒内有效垫球个数)进行整理，得到下列图表中信息：
垫球个数 | 频数 |
|
|
| 4 |
|
|
| 26 |
| 10 |
请根据所给信息，解答下列问题：
（1）
__________，
__________；
（2）这60名学生垫球个数的中位数落在__________段；
（3）全校报考排球项目女生共有450人，根据以往的经验垫球个数在30个以上(包含30个)在中考中能取得良好以上成绩，请估计中考体育考试中女生排球项目达到良好以上的女生人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我市公交总公司为节约资源同时惠及民生，拟对一些乘客数量较少的路线换成中巴车．该公司计划购买
台中巴车，现有甲、乙两种型号，已知购买一台甲型车比购买一台乙型车少万元，购买
台甲型车比购买
台乙型车多
万元．
（1）问购买一台甲型车和一台乙型车分别需要多少万元？
（2）经了解，每台甲型车每年节省费用
万元，每台乙型车每年节省费用
万元，若要使购买的这批中巴车每年至少能节省
万，则购买甲型车至少多少台？
查看答案和解析>>
科目：初中数学 来源： 题型：
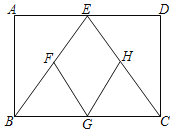
【题目】如图，已知四边形ABCD是矩形，点E，G分别是AD，BC边的中点，连接BE，CE，点F，H分别是BE，CE的中点连接FG，HG．
（1）求证：四边形EFGH是菱形；
（2）当
＝ 时，四边形EFGH是正方形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
