
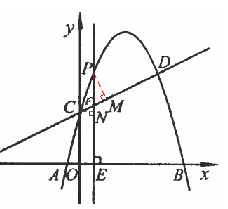
如图,抛物线 与直线
与直线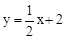 交于C,D两点,其中点C在y轴上,点D的坐标为
交于C,D两点,其中点C在y轴上,点D的坐标为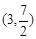 。点P是y轴右侧的抛物线上一动点,过点P作
。点P是y轴右侧的抛物线上一动点,过点P作 轴于点E,交CD于点F.
轴于点E,交CD于点F.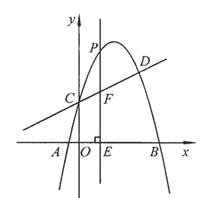
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O,C,P,F为顶点的四边形是平行四边形?请说明理由。
(3)若存在点P,使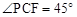 ,请直接写出相应的点P的坐标
,请直接写出相应的点P的坐标
(1)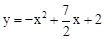 ;(2)当m=1或2或
;(2)当m=1或2或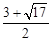 时,以O,C,P,F为顶点的四边形是平行四边形,理由见解析;(3)P(
时,以O,C,P,F为顶点的四边形是平行四边形,理由见解析;(3)P(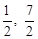 )或(
)或(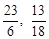 ).
).
解析试题分析:(1)由直线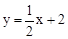 经过点C,求出点C的坐标;由抛物线
经过点C,求出点C的坐标;由抛物线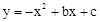 经过点C,D两点,用待定系数法即可求出抛物线的解析式;(2)因为PF∥CO,所以当PF=CO时,以O,C,P,F为顶点的四边形是平行四边形,分
经过点C,D两点,用待定系数法即可求出抛物线的解析式;(2)因为PF∥CO,所以当PF=CO时,以O,C,P,F为顶点的四边形是平行四边形,分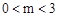 和
和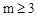 两种情况讨论即可;(3)如图,当点P在CD上方且∠PCF=450时,作PM⊥CD于点M,CN⊥PF于点N,则△PMF∽△CNF,∴
两种情况讨论即可;(3)如图,当点P在CD上方且∠PCF=450时,作PM⊥CD于点M,CN⊥PF于点N,则△PMF∽△CNF,∴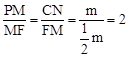 ,∴PM=CM=2CF,∴
,∴PM=CM=2CF,∴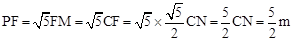 ,又∵
,又∵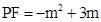 ,∴
,∴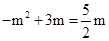 ,解得:
,解得: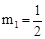 ,
,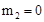 (舍去),∴P(
(舍去),∴P(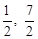 ),当点P在CD下方且∠PCF=450时,同理可以求得:另外一点为P(
),当点P在CD下方且∠PCF=450时,同理可以求得:另外一点为P(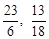 ).
).
试题解析:(1)∵直线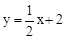 经过点C,∴C(0,2).
经过点C,∴C(0,2).
∵抛物线 经过点C(0,2),D
经过点C(0,2),D 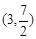 ,
,
∴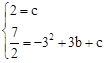 ,解得
,解得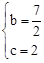 .
.
∴抛物线的解析式为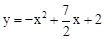 .
.
(2)∵点P的横坐标为m且在抛物线上, ∴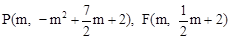 .
.
∵PF∥CO,∴当PF=CO时,以O,C,P,F为顶点的四边形是平行四边形.
当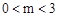 时,
时,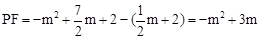 ,
,
∴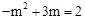 ,解得:
,解得: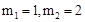 .
.
即当m=1或2时,四边形OCPF是平行四边形.
当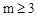 时,
时,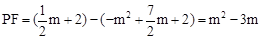 ,
,
∴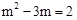 ,解得:
,解得: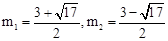 (∵点P在y轴右侧的抛物线上,∴舍去).
(∵点P在y轴右侧的抛物线上,∴舍去).
即当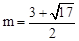 时,四边形OCFP是平行四边形.
时,四边形OCFP是平行四边形.
综上所述,当m=1或2或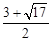 时,以O,C,P,F为顶点的四边形是平行四边形.
时,以O,C,P,F为顶点的四边形是平行四边形.
(3)P(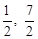 )或(
)或(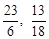 ).
).
考点:1.二次函数综合题;2.单动点问题;3.曲线上点的坐标与方程的关系;4.平行四边形的性质;5.相似三角形的判定和性质;6.分类思想的应用.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
已知:如图,抛物线 与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).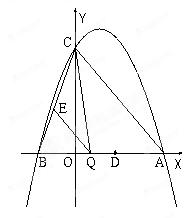
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(3)若平行于x轴的动直线 与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线
与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线 ,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线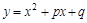 上有一点M(x0,
上有一点M(x0,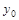 )位于
)位于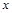 轴下方.
轴下方.
(1)求证:此抛物线与x轴交于两点;
(2)设此抛物线与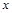 轴的交点为A(
轴的交点为A(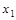 ,0),B(
,0),B(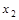 ,0),且
,0),且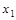 <
<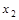 ,求证:
,求证: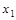 <
<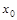 <
<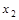 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数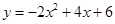 .
.
(1)求出该函数图象的顶点坐标,图象与x轴的交点坐标.
(2)当x在什么范围内时,y随x的增大而增大?
(3)当x在什么范围内时,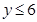 ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量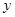 (件)与销售单价
(件)与销售单价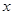 (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数: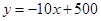 .
.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为 (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y=ax2+bx+3与x轴相交于点A(﹣1,0)、B(3,0),与y轴相交于点C,点P为线段OB上的动点(不与O、B重合),过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F,点D在y轴正半轴上,OD=2,连接DE、OF.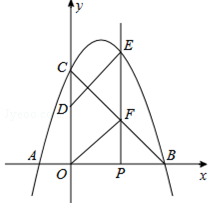
(1)求抛物线的解析式;
(2)当四边形ODEF是平行四边形时,求点P的坐标;
(3)过点A的直线将(2)中的平行四边形ODEF分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com