
【题目】某中学初三年级积极推进走班制教学。为了了解一段时间以来,“至善班”的学习效果,年级组织了多次定时测试,现随机选取甲、乙两个“至善班”,从中各抽取![]() 名同学在某一次定时测试中的数学成绩,其结果记录如下:
名同学在某一次定时测试中的数学成绩,其结果记录如下:
收集数据:
“至善班”甲班的![]() 名同学的数学成绩统计(满分为
名同学的数学成绩统计(满分为![]() 分) (单位:分)
分) (单位:分)

“至善班”甲=乙班的![]() 名同学的数学成绩统计(满分为
名同学的数学成绩统计(满分为![]() 分) (单位:分)
分) (单位:分)

整理数据:(成绩得分用![]() 表示)
表示)
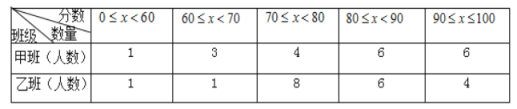
分析数据,并回答下列问题:
![]() 完成下表:
完成下表:
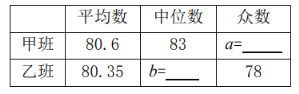
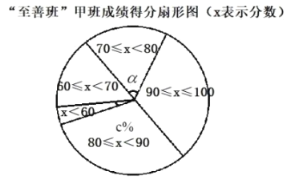
![]() 在“至善班”甲班的扇形图中,成绩在
在“至善班”甲班的扇形图中,成绩在![]() 的扇形中,说对的圆心角
的扇形中,说对的圆心角![]() 的度数为 .估计全部“至善班”的
的度数为 .估计全部“至善班”的![]() 人中优秀人数为 人.(
人中优秀人数为 人.(![]() 分及以上为优秀).
分及以上为优秀).
![]() 根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本的同学的学习效果更好一些,你所做判断的理由是:
根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本的同学的学习效果更好一些,你所做判断的理由是:
① .
② .
【答案】![]()
![]()
![]()
![]()
![]() ;
;![]()
![]() 甲,理由:甲的平均数高于乙,说明平均水平较好;甲的中位数高于乙,说明整体水平高.
甲,理由:甲的平均数高于乙,说明平均水平较好;甲的中位数高于乙,说明整体水平高.
【解析】
(1)根据众数以及中位数的概念即可求解.
(2)用360°乘70≤x<80的人数占总人数的比例可得成绩在![]() 的扇形中,说对的圆心角
的扇形中,说对的圆心角![]() 的度数,总人数乘以样本中80分及以上人数所占比例即可得.
的度数,总人数乘以样本中80分及以上人数所占比例即可得.
(3)根据平均数以及中位数进行判断即可.
![]() “至善班”甲班的
“至善班”甲班的![]() 名同学的数学成绩中,96分出现了3次,出现的次数最多,
名同学的数学成绩中,96分出现了3次,出现的次数最多,
则![]() ,
,
“至善班”乙班的![]() 名同学的数学成绩从小到大排列,54,60,70,72,75,76,76,78,78,78,80,82,82,86,87,87,92,96,98,100,
名同学的数学成绩从小到大排列,54,60,70,72,75,76,76,78,78,78,80,82,82,86,87,87,92,96,98,100,
中间两个数是78,80,则中位数是:![]()
即 ![]() .
.
![]() 成绩在
成绩在![]() 的扇形中,说对的圆心角
的扇形中,说对的圆心角![]() 的度数为:
的度数为:![]()
![]() :
:![]() (人)
(人)
![]() 甲;
甲;
理由:甲的平均数高于乙,说明平均水平较好;甲的中位数高于乙,说明整体水平高.


 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
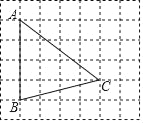
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长等于_____;
(Ⅱ)在线段AC上有一点D,满足AB2=ADAC,请在如图所示的网格中,用无刻度的直尺,画出点D,并简要说明点D的位置是如何找到的(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
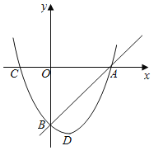
【题目】如图抛物线y=x2+bx-c经过直线y=x-3与坐标轴的两个交点A,B,与x轴交于另一点C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)求S△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,点D、E分别在边AC、AB上,∠ABD=∠ACE,下列条件中,不能判定△ABC是等腰三角形的是( )

A. AE=AD;B. BD=CE;C. ∠ECB=∠DBC ;D. ∠BEC=∠CDB.
查看答案和解析>>
科目:初中数学 来源: 题型:
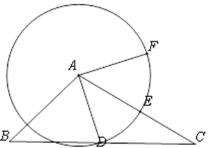
【题目】如图,已知△ABC,AB=![]() ,
,![]() ,∠B=45°,点D在边BC上,联结AD, 以点A为圆心,AD为半径画圆,与边AC交于点E,点F在圆A上,且AF⊥AD.
,∠B=45°,点D在边BC上,联结AD, 以点A为圆心,AD为半径画圆,与边AC交于点E,点F在圆A上,且AF⊥AD.
(1)设BD为x,点D、F之间的距离为y,求y关于x的函数解析式,并写出定义域;
(2)如果E是![]() 的中点,求
的中点,求![]() 的值;
的值;
(3)联结CF,如果四边形ADCF是梯形,求BD的长 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级两个班,各选派10名学生参加学校举行的“美丽绍兴乡土风情知识”大赛预赛各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八(1)班 | 100 | m | 93 | 93 | 12 |
八(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)求表中m、n的值;
(2)依据数据分析表,有同学说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有同学说(2)班的成绩更好请您写出两条支持八(2)班成绩好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知:![]() 是圆
是圆![]() 的直径,
的直径,![]() ,点
,点![]() 为圆
为圆![]() 上异于点
上异于点![]() 、
、![]() 的一点,点
的一点,点![]() 为弦
为弦![]() 的中点.
的中点.
(1)如果![]() 交
交![]() 于点
于点![]() ,求
,求![]() :
:![]() 的值;
的值;
(2)如果![]() 于点
于点![]() ,求
,求![]() 的正弦值;
的正弦值;
(3)如果![]() ,
,![]() 为
为![]() 上一动点,过
上一动点,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,与射线
,与射线![]() 交于圆内点
交于圆内点![]() ,请完成下列探究.
,请完成下列探究.
探究一:设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式及其定义域.
的函数解析式及其定义域.
探究二:如果点![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上,写出此时
为半径的圆上,写出此时![]() 的长度.
的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
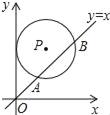
【题目】如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2![]() ,则a的值是_____.
,则a的值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com