
����Ŀ����ͼ����֪![]() ��
��![]() ��
��![]() ���ĺ�������1�и����˼���
���ĺ�������1�и����˼���![]() ��
��![]() �Ķ�Ӧֵ��
�Ķ�Ӧֵ��
��1��
| �� |
| 1 |
| 2 |
| 3 | �� |
| �� | 6 | 3 | 2 |
|
| 1 | �� |

��1���Ա��и��Զ�ӦֵΪ���꣬��ͼ1��ֱ������ϵ��������㣬�ù⻬����˳������.��ͼ��֪�����������Ѿ�ѧ�������ຯ���������������ʽ����ֱ��д��![]() ��ֵ��
��ֵ��
��2�����һ�κ���ͼ���루1����ͼ����![]() ��
��![]() ���㣬�ڵ�һ���������ڵ�
���㣬�ڵ�һ���������ڵ�![]() ��ʲô��Χʱ��һ�κ�����ֵС�ڣ�1���к�����ֵ����ֱ��д����.
��ʲô��Χʱ��һ�κ�����ֵС�ڣ�1���к�����ֵ����ֱ��д����.
���𰸡���1����ͼ�����������Ƿ�����������![]() ��
��![]() ����2��
����2��![]() ��
��![]() .
.
��������
��1���������Ľ�����ù⻬����˳�����Ӽ��ɵõ�����ͼ��Ϊ˫���ߵ�һ֧���ٸ��ݷ���������ͼ���ϵ�������������ɵõ�a��ֵ��
��2�����ú���ͼ���ɵõ�һ�κ�����ֵС�ڣ�1���к�����ֵʱx��ȡֵ��Χ��
�⣺��1����ͼ��ʾ��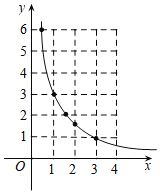
��ͼ��֪��xy=3�������Ƿ���������y��![]() ��
��
��x=![]() ʱ��y=
ʱ��y=![]() ��
��
��a=![]() ��
��
��2���ڵ�һ�����ڣ���0��x��1��x��3ʱ��һ�κ�����ֵС�ڷ�����������ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
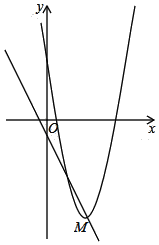
����Ŀ����ƽ��ֱ������ϵ�У�������![]() �Ķ���M��ֱ��L��
�Ķ���M��ֱ��L��![]() �ϣ�
�ϣ�
![]() ��ֱ��L�ĺ�������ʽ��
��ֱ��L�ĺ�������ʽ��
![]() �ֽ��������ظ�ֱ��L�������ƽ�ƣ�ƽ�ƺ�������ߵĶ���ΪN����x����ҽ���ΪC������NC����
�ֽ��������ظ�ֱ��L�������ƽ�ƣ�ƽ�ƺ�������ߵĶ���ΪN����x����ҽ���ΪC������NC����![]() ʱ����ƽ�ƺ�������ߵĽ���ʽ��
ʱ����ƽ�ƺ�������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
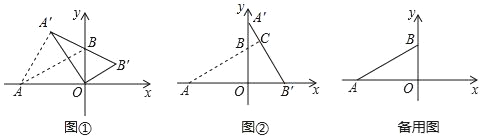
����Ŀ����ƽ��ֱ������ϵ�У�OΪԭ�㣬��A����![]() ��0������B��0��1���ѡ�ABO�Ƶ�O˳ʱ����ת���á�A'B'O����A��B��ת��Ķ�Ӧ��ΪA'��B'������ת��Ϊ����0�㣼����360�㣩��
��0������B��0��1���ѡ�ABO�Ƶ�O˳ʱ����ת���á�A'B'O����A��B��ת��Ķ�Ӧ��ΪA'��B'������ת��Ϊ����0�㣼����360�㣩��
��1����ͼ�٣�����A�䣬B��B�乲��ʱ����AA��ij���
��2����ͼ�ڣ�������90�㣬��ֱ��AB��A��B��Ľ���C�����ꣻ
��3������A����ֱ��AB��ʱ����BB����OA��Ľ���D�����ֱ꣨��д��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣���ͼ����֪O������ԭ�㣬B��C���������ֱ�Ϊ��3����1������2��1����

��1����O��Ϊλ��������y�����ཫ��OBC�Ŵ���������ͼ�Ρ�
��2��д��B��C����Ķ�Ӧ��B��C�����ꣻ
��3�������OBC�ڲ�һ��M������Ϊ(x��y)��д��M�Ķ�Ӧ��M�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij���˲���������һ�����ʣ��������ʹ���4Сʱ����������2Сʱ��ʼ�������ʣ�����������������ʵ��ٶȾ����ֲ��䣩.���˲��������![]() ���֣���ʱ��
���֣���ʱ��![]() ��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ���������ʴӿ�ʼ������ȫ��������Ҫ��ʱ���ǣ� ��
��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ���������ʴӿ�ʼ������ȫ��������Ҫ��ʱ���ǣ� ��
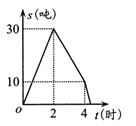
A. 4СʱB. 4.3СʱC. 4.4СʱD. 5Сʱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ƶ��ն���������������,�ֻ��Ѿ���Ϊ���������в���ȱ�ٵ�һ����,Ϊ�˽���ѧ���ڼ���ʹ���ֻ������(ѡ����A .��ͬѧ�������죻B.ѧϰ��C.���D.��Ϸ��E.������,����ں�ij��ѧ��ȫУ��Χ�������ȡ��������ѧ�����е���,�õ�����ͼ����������Ϣδ������:

����������Ϣ�����������:
��1����α������ѧ���ж����ˣ�
��2�������![]() ��ֵ������ȫ����ͳ��ͼ��
��ֵ������ȫ����ͳ��ͼ��
��3��������ѧԼ��![]() ��ѧ��������ȫУѧ���������ֻ����������Ϸ�Ĺ��ж����ˣ�
��ѧ��������ȫУѧ���������ֻ����������Ϸ�Ĺ��ж����ˣ�
���������ϵ������������ѧ����κ���ʹ���ֻ��������һ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ��ֱ��
��ֱ��![]() ����
����![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ���������ߵ���һ������Ϊ
���������ߵ���һ������Ϊ![]() ����
����![]() ���ڵ�
���ڵ�![]() .���
.���![]() ��ֱ��
��ֱ��![]() �Ϸ�����������һ���㣨�����
�Ϸ�����������һ���㣨�����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��
��![]() ���ƽ���ߣ���ֱ��
���ƽ���ߣ���ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() .
.

��1����գ�![]() __________��
__________��![]() __________��
__________��![]() __________��
__________��
��2��̽�����Ƿ���������ĵ�![]() ��ʹ�ı���
��ʹ�ı���![]() ��ƽ���ı��Σ������ڣ��������
��ƽ���ı��Σ������ڣ��������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
��3����![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ����
����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ�������
�ĺ�����ϵʽ�������![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�����ų�Ϊ5,��Ϊ1�ľ���ֽ������,���������ζԽ��߽����غ�,��ʹ�ص����ֳ�Ϊһ������.������ֽ����ֱʱ,�����ܳ�����Сֵ��4,��һ�����������������غϵĶԽ��߽�����תһ���Ƕ�,����ת������,�ó������ص�����Ϊ���ε��ı�����,�ܳ������ֵ��(����)

A. 8B. 10C. 10.4D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
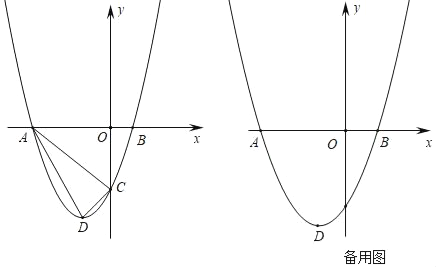
����Ŀ����ͼ��������y��ax2+2ax��3a��a��0����x����A��B���㣬��y���ڵ�C�������ߵĶ���ΪD��
��1����գ������ߵĶԳ���Ϊ�� ������A������Ϊ�� ������B������Ϊ�� ����
��2������ADC�����Ϊ3���������ߵĽ���ʽ��
��3���ڣ�2���������£���m��x��m+1��y��ȡֵ��Χ�ǩ�4��y��2m����m��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com