
 如图所示,在△ABC中,中线BD、CE交于O,F、G分别是OB、OC的中点,求证:EG、FD互相平分.
如图所示,在△ABC中,中线BD、CE交于O,F、G分别是OB、OC的中点,求证:EG、FD互相平分. 分析 利用三角形中线的性质、中位线的定义和性质证得四边形EFGD的对边DE∥GF,且DE=GF=$\frac{1}{2}$BC;然后由平行四边形的判定--对边平行且相等的四边形是平行四边形,证得结论.
解答 证明:∵BD、CE是△ABC的两条中线,
∴点D、E分别是边AC、AB的中点,
∴DE∥CB,DE=$\frac{1}{2}$CB;
又∵F、G分别是OB、OC的中点,
∴GF∥CB,GF=$\frac{1}{2}$CB;
∴DE∥GF,且DE=GF,
∴四边形DEFG是平行四边形,
∴EG、FD互相平分.
点评 本题考查了三角形中位线定理、平行四边形的判定.平行四边形的判定:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;一组对边平行,一组对角相等的四边形是平行四边形.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
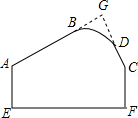 如图所示的模板,按规定AB,CD的延长线交成80°的角,因交点不在板上,测量后质检员测得∠BAE=122°,∠DCF=155°,如果你是质检员,如何知道模板是否合格?为什么?
如图所示的模板,按规定AB,CD的延长线交成80°的角,因交点不在板上,测量后质检员测得∠BAE=122°,∠DCF=155°,如果你是质检员,如何知道模板是否合格?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com