
【题目】在数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,且a,c满足|a+2|+(c-7)2=0.
(1)填空:a=________,b=________,c=________;
(2)画出数轴,并把A,B,C三点表示在数轴上;
(3)P是数轴上任意一点,点P表示的数是x,当PA+PB+PC=10时,x的值为多少?
【答案】 -2 1 7
【解析】
(1)根据非负数的性质列方程求出a、c的值,根据有理数的概念求出b的值,从而得解;
(2)根据数轴的定义画图并表示即可;
(3)根据数轴上两点间的距离公式得出一个绝对值方程,然后分x≤2、-2<x≤1、1<x≤7和x>7四种情况去掉绝对值即可求出x的值.
解:(1)由题意可知a+2=0,c-7=0,
解得a=-2,c=7.
因为b是最小的正整数,所以b=1.
故答案为-2,1,7.
(2)画出数轴如图所示:
![]()
(3)因为PA+PB+PC=10,所以|x+2|+|x-1|+|x-7|=10.
当x≤-2时,-x-2+1-x+7-x=10,
解得x=-![]() (舍去).
(舍去).
当-2<x≤1时,x+2+1-x+7-x=10,
解得x=0.
当1<x≤7时,x+2+x-1+7-x=10,
解得x=2.
当x>7时,x+2+x-1+x-7=10,
解得x=![]() (舍去).
(舍去).
综上所述,当PA+PB+PC=10时,x的值是0或2.


科目:初中数学 来源: 题型:
【题目】把下列各数填入相应的括号内:11,-![]() ,6.5,-8,3
,6.5,-8,3![]() ,0,1,-1,-3.14.
,0,1,-1,-3.14.
(1)正数集合:{ …};(2)负数集合:{ …};
(3)整数集合:{ …};(4)正整数集合:{ …};
(5)负整数集合:{ …};(6)分数集合:{ …};
(7)正分数集合:{ …};(8)负分数集合:{ …};
(9)有理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )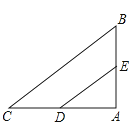
A.相切
B.相交
C.相离
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是以数轴原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,求OP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-24×![]() ;
;
(2)-9+5×(-6)-(-4)2÷(-8);
(3)0.25×(-2)2-[4÷![]() +1]+(-1)2018;
+1]+(-1)2018;
(4)-42÷![]() -[
-[![]() ].
].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=![]() 和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.

【答案】8![]()
【解析】整体分析:
联立方程y=![]() 和y= - x+4,求出点A,B的坐标,然后由公式△OAB的面积=
和y= - x+4,求出点A,B的坐标,然后由公式△OAB的面积=![]() ×(x1- x2)(y2- y1)求解.
×(x1- x2)(y2- y1)求解.
解:把y=![]() 代入y= - x+4得,
代入y= - x+4得,
![]() = - x+4,
= - x+4,
解得x1=2+![]() ,x2=2-
,x2=2-![]() .
.
所以y1=2-![]() ,y2=2+
,y2=2+![]() .
.
则A(2-![]() ,2+
,2+![]() ),B(2+
),B(2+![]() ,2-
,2-![]() ),
),
所以△OAB的面积=![]() ×(x1- x2)(y2- y1)==
×(x1- x2)(y2- y1)==![]() ×4
×4![]() ×4
×4![]() =
=![]() .
.
【题型】解答题
【结束】
19
【题目】如图,直线![]() 与双曲线
与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.

(1)求m及k的值;
(2)不解关于x、y的方程组 直接写出点B的坐标;
直接写出点B的坐标;
(3)直线![]() 经过点B吗?请说明理由.
经过点B吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图17-Z-10是由边长为1的小正方形组成的网格.
(1)求四边形ABCD的面积;
(2)你能判断AD与CD的位置关系吗?说出你的理由.

图17-Z-10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠A+∠D=180°,∠1=3∠2,∠2=24°,点P是BC上的一点.
(1)请写出图中∠1的一对同位角,一对内错角,一对同旁内角;
(2)求∠EFC与∠E的度数;
(3)若∠BFP=46°,请判断CE与PF是否平行?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( ).
A. m=-2是方程m-2=0的解 B. m=6是方程3m+18=0的解
C. x=-1是方程-![]() =0的解 D. x=
=0的解 D. x=![]() 是方程10x=1的解
是方程10x=1的解
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com