
【题目】如图,已知反比例函数y=![]() 的图象与正比例函数y=kx的图象交于点A(m,﹣2).
的图象与正比例函数y=kx的图象交于点A(m,﹣2).
(1)求正比例函数的解析式及两函数图象另一个交点B的坐标;
(2)试根据图象写出不等式![]() ≥kx的解集;
≥kx的解集;
(3)在反比例函数图象上是否存在点C,使△OAC为等边三角形?若存在,求出点C的坐标;若不存在,请说明理由.
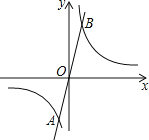
【答案】(1)y=2x;B(1,2)
(2)①当x>0时,2x2≤2,解得0<x≤1,
②当x<0时,2x2≥2,解得x≤﹣1;
(3)不存在,见解析
【解析】
试题解析:(1)把A(m,﹣2)代入y=![]() ,得﹣2=
,得﹣2=![]() ,解得m=﹣1,
,解得m=﹣1,
∴A(﹣1,﹣2)代入y=kx,
∴﹣2=k×(﹣1),解得,k=2,
∴y=2x,
又由2x=![]() ,得x=1或x=﹣1(舍去),
,得x=1或x=﹣1(舍去),
∴B(1,2),
(2)∵k=2,
∴![]() ≥kx即为
≥kx即为![]() ≥kx
≥kx
①当x>0时,2x2≤2,解得0<x≤1,
②当x<0时,2x2≥2,解得x≤﹣1;
(3)①当点C在第一象限时,△OAC不可能为等边三角形,
②如图,当C在第三象限时,要使△OAC为等边三角形,则|OA|=|OC|,设C(t,)(t<0),

∵A(﹣1,﹣2)
∴OA=![]()
∴t2+![]() =5,则t4﹣5t2+4=0,
=5,则t4﹣5t2+4=0,
∴t2=1,t=﹣1,此时C与A重合,舍去,
t2=4,t=﹣2,C(﹣2,﹣1),而此时|AC|=![]() ,|AC|≠|AO|,
,|AC|≠|AO|,
∴不存在符合条件的点C.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广节能灯,为响应号召,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10公分.如图2,若此钟面显示3点45分时,A点距桌面的高度为16公分,则钟面显示3点50分时,A点距桌面的高度为多少公分()
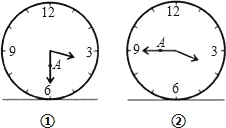
A. ![]() B. 16+π C. 18 D. 19
B. 16+π C. 18 D. 19
查看答案和解析>>
科目:初中数学 来源: 题型:
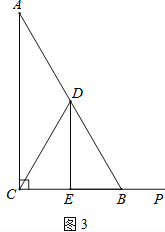
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 ;
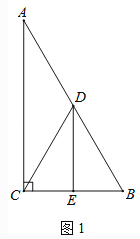
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
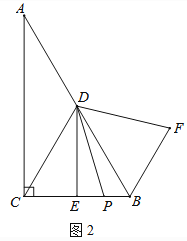
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
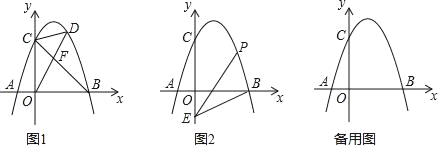
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
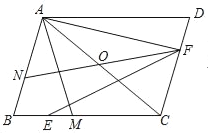
【题目】如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.
(1)若BM=4,MC=3,AC=![]() ,求AM的长度;
,求AM的长度;
(2)若∠ACB=45°,求证:AN+AF=![]() EF.
EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
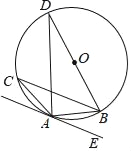
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2,求AD的长.
,AC=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药厂两年前生产1t某种药品的成本是5000元,随着生产技术的进步,现在生产1t该种药品的成本是3000元.设该种药品生产成本的年平均下降率为x,则下列所列方程正确的是( )
A. 5000×2(1﹣x)=3000 B. 5000×(1﹣x)2=3000
C. 5000×(1﹣2x)=3000 D. 5000×(1﹣x2)=3000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com