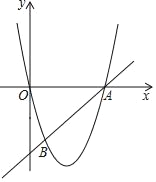
【题目】如图，在平面直角坐标系xOy中，直线AB与抛物线y＝ax2+bx交于点A（6，0）和点B（1，﹣5）．
（1）求这条抛物线的表达式和直线AB的表达式；
（2）如果点C在直线AB上，且∠BOC的正切值是
，求点C的坐标．
【答案】（1）y＝x2﹣6x，y＝x﹣6；（2）C（
，﹣
）．
【解析】
（1）利用待定系数法求二次函数和一次函数的解析式；
（2）先说明OA=OH=6，则∠OAH=45°，作辅助线，根据正切值证明∠BOC=∠OBE，作OB的垂直平分线交AB于C，交OB于F，解法一：先根据中点坐标公式可得F（
），易得直线OB的解析式为：y=﹣5x，根据两直线垂直的关系可得直线FC的解析式为：y
，列方程
x﹣6，解出可得C的坐标；
解法二：过C作CD⊥x轴于D，连接OC，设C（m，m﹣6），根据OC=BC，列方程可得结论．
（1）把点A（6，0）和点B（1，﹣5）代入抛物线y=ax2+bx得：
，解得：
，∴这条抛物线的表达式：y=x2﹣6x，设直线AB的解析式为：y=kx+b，把点A（6，0）和点B（1，﹣5）代入得：
，解得：
，则直线AB的解析式为：y=x﹣6；
（2）当x=0时，y=6，当y=0时，x=6，∴OA=OH=6．
∵∠AOH=90°，∴∠OAH=45°，过B作BG⊥x轴于G，则△ABG是等腰直角三角形，∴AB=5
，过O作OE⊥AB于E，S△AOH
AHOEOAOH，6OE=6×6，OE=3，∴BE=AB﹣AE=5
，Rt△BOE中，tan∠OBE
．
∵∠BOC的正切值是
，∴∠BOC=∠OBE，∴OC=CB．作OB的垂直平分线交AB于C，交OB于F，解法一：∵B（1，﹣5），∴F（），易得直线OB的解析式为：y=﹣5x，设直线FC的解析式为：y
x+b，把F（）代入得：
b，b
，∴直线FC的解析式为：y
x﹣6，x
，当x时，y
，∴C（
）；
解法二：过C作CD⊥x轴于D，连接OC，设C（m，m﹣6），则AC
（6﹣m）．
∵OC=BC，∴m2+（m﹣6）2=[5
（6﹣m）]，m，∴C（）．
科目：初中数学 来源： 题型：
【题目】在
，
中，
，连接
，
是中点，连接
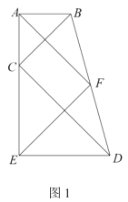
（1）如图1，若
三点在同一直线上，
，已知
，求线段
的长；
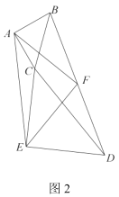
（2）如图2，若，求证：
为等腰直角三角形；
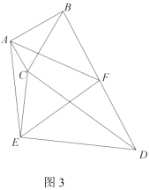
（3）如图3，若
，请判断的形状，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】平行四边形ABCD中，E，F是对角线BD上的两点， 如果添加一个条件使△ABE≌△CDF，则添加的条件不能是（ ）
A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目：初中数学 来源： 题型：
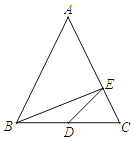
【题目】如图，在△ABC中，AB＝AC，BC＝6，E为AC边上的点且AE＝2EC，点D在BC边上且满足BD＝DE，设BD＝y，S△ABC＝x，则y与x的函数关系式为( )
A.y＝
x2+
B.y＝
x2+
C.y＝x2+2D.y＝x2+2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点
是
直径
上的一点，过作直线
，分别交于
，
两点，连接
，并将线段绕点
逆时针旋转
得到
，连接
，分别交和于
，
，连接
．
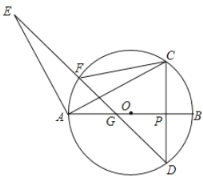
（Ⅰ）求证：
；
（Ⅱ）若点在直径上运动（不与点，
重合），其它条件不变，请问
是否为定值？若是，请求出其值；若不是，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校九年级共有80名同学参与数学科托底训练．其中（1）班30人，（2）班25人，（3）班25人，吕老师在托底训练后对这些同学进行测试，并对测试成绩进行整理，得到下面统计图表．
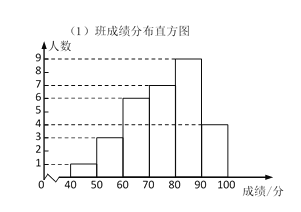
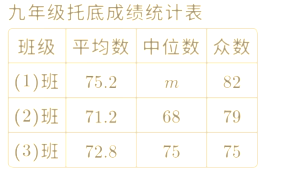
（1）表格中的m落在________组；（填序号）
①40≤x＜50， ②50≤x＜60， ③60≤x＜70，
④70≤x＜80， ⑤80≤x＜90， ⑥90≤x≤100．
（2）求这80名同学的平均成绩；
（3）在本次测试中，（2）班小颖同学的成绩是70分，（3）班小榕同学的成绩是74分，这两位同学成绩在自己所在班级托底同学中的排名，谁更靠前？请简要说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
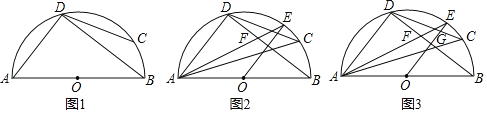
【题目】已知半圆O，点C、D在弧AB上，连接AD、BD、CD，∠BDC+2∠ABD＝90°．
（1）如图1，求证：DA＝DC；
（2）如图2，作OE⊥BD交半圆O于点E，连接AE交BD于点F，连接AC，求证：∠DFA＝∠DAC+∠DAE；
（3）如图3，在（2）的条件下，设AC交BD于点G，FG＝1，AG＝5，求半圆O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，抛物线y＝a（x+2）（x﹣6）（a＞0）与x轴交于C，D两点（点C在点D的左边），与y轴负半轴交于点A．
如图1，抛物线y＝a（x+2）（x﹣6）（a＞0）与x轴交于C，D两点（点C在点D的左边），与y轴负半轴交于点A．
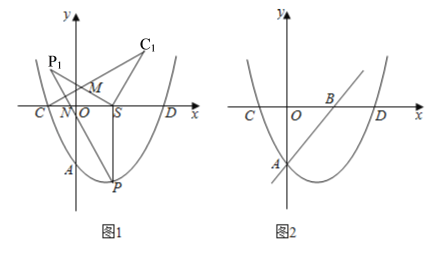
（1）若△ACD的面积为16．
①求抛物线解析式；
②S为线段OD上一点，过S作x轴的垂线，交抛物线于点P，将线段SC，SP绕点S顺时针旋转任意相同的角到SC1，SP1的位置，使点C，P的对应点C1，P1都在x轴上方，C1C与P1S交于点M，P1P与x轴交于点N．求
的最大值；
（2）如图2，直线y＝x﹣12a与x轴交于点B，点M在抛物线上，且满足∠MAB＝75°的点M有且只有两个，求a的取值范围．
（1）若△ACD的面积为16．
①求抛物线解析式；
②S为线段OD上一点，过S作x轴的垂线，交抛物线于点P，将线段SC，SP绕点S顺时针旋转任意相同的角到SC1，SP1的位置，使点C，P的对应点C1，P1都在x轴上方，C1C与P1S交于点M，P1P与x轴交于点N．求的最大值；
（2）如图2，直线y＝x﹣12a与x轴交于点B，点M在抛物线上，且满足∠MAB＝75°的点M有且只有两个，求a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
