
如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1,∠BAE=30°.

(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB'E'(如图2),使点E落在CD边上的点E'处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
(1)证明见解析;
(2) ;
;
(3)没有变化,理由见解析.
【解析】
试题分析:(1)要证△ABE≌△BCF,已知条件是AB=BC ,∠ABE=∠BCF=90°,只需要再有一条边或一个角对应相等即可,而通过已知条件可以得到∠BAE=∠CBF,利用ASA即可证全等了;
(2)由(1)△ABE≌△BCF,可得∠FBC=∠BAE=30°,又BE=1,∠BGE=90°,从而可得GE= ,利用勾股定理可得GB的长,从而可得△BEG)的面积;
,利用勾股定理可得GB的长,从而可得△BEG)的面积;
(3)由已知条件可得Rt△ABE≌Rt△AB'E'≌Rt△AD E', △BAG≌△HAG,从而可得S四边形B’E’HG=S△AB’E’-S三角形AGH=S△ABE-S△ABG=S△BEG,即重叠部分的面积没有变化.
试题解析:⑴∵正方形ABCD中,∠ABE=∠BCF=90°,AB=BC,
∴∠ABF+∠CBF=900,∵AE⊥BF, ∴∠ABF+∠BAE=900,
∴∠BAE=∠CBF, ∴△ABE≌△BCF.
⑵∵△ABE≌△BCF,∴∠FBC=∠BAE=30°,∵BE=1,∠BGE=90°,∴GE= ,∴GB=
,∴GB= =
=
∴S△BGE= ×
× ×
× =
= .
.
(3)没有变化,易证Rt△ABE≌Rt△AB'E'≌Rt△AD E', △BAG≌△HAG,
∴S四边形B’E’HG=S△AB’E’-S三角形AGH=S△ABE-S△ABG=S△BEG
∴△ABE在旋转前后与△BCF重叠部分的面积没有变化.
考点:1、正方形的性质;2、三角形全等的判定与性质;3、旋转的性质;4、勾股定理.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年山东潍坊高密四中文慧学校九年级上学期第一次月考数学试卷(解析版) 题型:选择题
D为△ABC边AB上一点,下列说法中错误的是 ( )
A.若∠ACD=∠B,则△ACD∽△ABC B.若∠ADC=∠ACB,则△ACD∽△ABC
C.若AC2=AD·AB,则△ACD∽△ABC D.若AC:CD=AB:BC, 则△ACD∽△ABC
查看答案和解析>>
科目:初中数学 来源:2014-2015学年天津市九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,抛物线
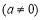 的对称轴为直线
的对称轴为直线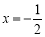 .下列结论中,正确的是( )
.下列结论中,正确的是( )
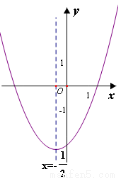
A.a<0
B.当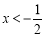 时, y随x的增大而增大
时, y随x的增大而增大
C.
D.当 时,y的最小值是
时,y的最小值是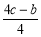
查看答案和解析>>
科目:初中数学 来源:2014-2015学年上海市闸北九年级期末考试数学试卷(解析版) 题型:解答题
(本题满分10分, 第(1)小题6分,第(2)小题4分)
已知二次函数 的图像经过点A(0,4)和B(1,-2).
的图像经过点A(0,4)和B(1,-2).
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为y=a(x+m)2+k的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省七校九年级上学期联考数学试卷(解析版) 题型:选择题
如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则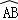 的长为( )
的长为( )

A.π B. 6π C. 3π D. 1.5π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com