
【题目】如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=__.

【答案】4或6.
【解析】作出图形,然后分①点N在AC上,分AM和AB与AC是对应边两种情况,利用相似三角形对应边成比例列式求解即可;②点N在BC上,求出BM,再分BM和AB与BC是对应边,利用相似三角形对应边成比例列式求解即可.
解:如图所示,
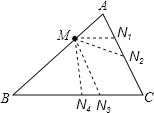
①点N在AC上,若AM和AB是对应边,
∵△AMN∽△ABC,
∴![]() ,即
,即![]() ,
,
解得MN=4,
若AM和AC是对应边,
∵△AMN∽△ACB,
∴![]() ,即
,即![]() ,
,
解得MN=6;
②点N在BC上,BM=AB-AM=9-3=6,
若BM和AB是对应边,
∵△MBN∽△ABC,
∴![]() ,即
,即![]() ,
,
解得MN=4,
若BM和BC是对应边,
∵△NBM∽△ABC,
∴![]() ,即
,即![]() ,
,
解得MN=3,
综上所述,MN的长为3或4或6.
“点睛”本题考查了相似三角形的判定,主要利用了相似三角形的对应边成比例,难点在于分情况讨论,作出图形更形象直观.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC=
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC=![]() .
.
(1)求该反比例函数和一次函数的解析式.
(2)求△BOC的面积.
(3)P是x轴上的点,且△PAC的面积与△BOC的面积相等,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机进货量的一半.电视机与洗衣机的进价和售价如下表:
类 别 | 电视机 | 洗衣机 |
进价(元/台) | 1 800 | 1 500 |
售价(元/台) | 2 000 | 1 600 |
计划购进电视机和洗衣机共 100 台,商店最多可筹集资金161 800 元.
(1)请你帮助商店算一算有多少种进货方案(不考虑除进价之外的其他费用);
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最大的利润(利润=售价-进价).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A,B两点,若反比例函数![]() (x>0)的图像与△ABC有公共点,则k的取值范围是( )
(x>0)的图像与△ABC有公共点,则k的取值范围是( )
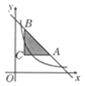
A. 2≤k≤8 B. 2≤k≤9 C. 2≤k≤5 D. 5≤k≤8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班6个同学在课间体育活动时进行1分钟跳绳比赛,成绩如下:126,144,134,118,126,152.这组数据中,众数和中位数分别是( )
A.126,126
B.130,134
C.126,130
D.118,152
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC放置在平面直角坐标系中,已知A(0,0)、B(2,0),反比例函数的图象经过点C.
(1)求点C的坐标及反比例函数的解析式.
(2)如果将等边△ABC向上平移n个单位长度,使点B恰好落在双曲线上,求n的值.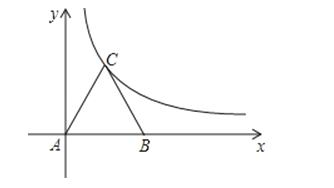
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出下列函数关系式,并指出其中的反比例函数及正比例函数.
(1)当圆柱的体积是50cm3时,他的高h(cm)与底面圆的面积S(cm2)的关系;
(2)玲玲用200元钱全部用来买营养品送给她妈妈,那么她所能购买营养品的数量y(kg)与单价x(元/kg)的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com